2020AMC10A - 数学 (10)

2020 AMC 10A 试题/第1题

第1题

满足条件的 $ x $ 的值为多少？

\[ x - \frac{3}{4} = \frac{5}{12} - \frac{1}{3}? \]

(A) $ - \frac{2}{3} $ (B) $ \frac{7}{36} $ (C) $ \frac{7}{12} $ (D) $ \frac{2}{3} $ (E) $ \frac{5}{6} $

解答

两边同时加上 $ \frac{3}{4} $ ，

$ x = \frac{5}{12} - \frac{1}{3} + \frac{3}{4} = \frac{5}{12} - \frac{4}{12} + \frac{9}{12} = 0\left( \mathbf{E}\right) \frac{5}{6}. $

2020 AMC 10A 试题/第2题

第2题

数 $ 3,5,7, a, $ 与 $ b $ 的平均值(算术平均数)为15，求 $ a $ 与 $ b $ 的平均值。

(A) 0 (B) 15 (C) 30 (D) 45 (E) 60

解答

数 $ 3,5,7, a, $ 与 $ b $ 的算术平均数等于 $ \frac{3 + 5 + 7 + a + b}{5} = \frac{{15} + a + b}{5} = {15} $ 。解得 $ a + b $ ，从而 $ a + b = {60} $ 。将 $ a $ 与 $ b $ 相加后除以2，得到平均值 $ \frac{60}{2} = $ (C)30

2020 AMC 10A 试题/第3题

第3题

假设 $ a \neq 3 $ 、 $ b \neq 4 $ 和 $ c \neq 5 $ ，则下列表达式的最简值是多少？

\[ \frac{a - 3}{5 - c} \cdot \frac{b - 4}{3 - a} \cdot \frac{c - 5}{4 - b} \]

(A) -1 (B) 1 (C) $ \frac{abc}{60} $ (D) $ \frac{1}{abc} - \frac{1}{60} $ (E) $ \frac{1}{60} - \frac{1}{abc} $

解答

注意是乘以。同样，是乘以 $ 4 - b $ ，并且是

乘以 $ 5 - c $ 。因此，给定分数的乘积等于

2020 AMC 10A 试题/第4题

题目

一位司机以每小时60英里(miles per hour)的速度行驶2小时，期间她的汽车每加仑(gallon)汽油可行驶30英里(miles per gallon)。她每英里获得 $ \ $ {0.50} $ 美元，唯一支出是每加仑 $ \ $ {2.00} $ 美元的汽油费。扣除这笔费用后，她的净时薪是多少美元/小时？

(A) 20 (B) 22 (C) 24 (D) 25 (E) 26 解答

由于司机每小时行驶60英里，每小时耗油2加仑，因此她每小时在汽油上花费 $ \ $ 4 $ 美元。如果她每英里获得 $ \ $ {0.50} $ 美元，则每小时

驾驶可获得美元。扣除油费后，她的净时薪为 $ \sigma $ 美元。减去

2020 AMC 10A 试题/第5题

第5题

求所有满足 $ \left| {{x}^{2} - {12x} + {34}}\right| = 2 $ 的实数 $ x $ 之和。

(A) 12 (B) 15 (C) 18 (D) 21 (E) 25 解答1

将方程拆分为两种情况:绝对值内的值为正和非正。

情况1:

方程得到 $ {x}^{2} - {12x} + {34} = 2 $ ，等于

$ \left( {x - 4}\right) \left( {x - 8}\right) = 0 $ 因此，正数情况下的两个值为4和8。

情况2:

类似地，对绝对值符号内的值取非正情况得到 $ - {x}^{2} + {12x} - {34} = 2 $ 。因式分解并化简得 $ {\left( x - 6\right) }^{2} = 0 $ ，因此该情况下的唯一值为6。

将所有值相加得到 $ 4 + 8 + 6 = {(C}){18} $ 。

解法2

我们有方程 $ {x}^{2} - {12x} + {32} = 0 $ 和 $ {x}^{2} - {12x} + {36} = 0 $ 。

注意到第二个方程是完全平方，在 $ x = 6 $ 处有二重根，而第一个方程有实根。根据韦达定理(Vieta’s formulas)，第一个方程的根之和为12。

\[ {12} + 6 = \left( \begin{array}{l} \mathrm{C} \end{array}\right) {18} \]

2020 AMC 10A 试题/第6题

题目

有多少个4位正整数(即介于1000到9999之间，含端点)的所有数字均为偶数且能被5整除？

(A) 80 (B) 100 (C) 125 (D) 200 (E) 500

解答

对于所有能被5整除的数，个位必须是0或5。然而，根据题设限制，该位必须为偶数，因此个位只有唯一选择(0)。对于中间两位，可从 $ \left\lbrack {0,8}\right\rbrack $ 中任选一个偶数，即共有5种选择。对于首位，同理可知其不能为0，因此有4种可能。于是，根据乘法原理，我们得到 $ 4 \times 5 \times 5 \times 1 = \left| {\text{(B) }{100}}\right| $ 。~ciceronii

2020 AMC 10A 试题/第7题

以下题目同时出现在2020 AMC 12A第5题和2020 AMC 10A第7题，因此两题均重定向至此页。

题目

从-10到14(含)的25个整数可以排成一个5×5方阵，使得每一行、每一列以及两条主对角线上的数字之和都相同。这个共同的和是多少？

(A) 2 (B) 5 (C) 10 (D) 25 (E) 50

解决方案

不失一般性，考虑该方阵中的五行。每行的数字之和必须相等，这意味着方阵中所有数字之和除以5即为每行的总值。这25个整数的总和为

$ - {10} + 9 + \ldots + {14} = {11} + {12} + {13} + {14} = {50} $ ，以及常见的

总和为 $ \frac{50}{5} = $ (C)10。

解决方案 2

取该集合中间5个值之和(它们最终将成为每一行的平均值)。我们得到 $ 0 + 1 + 2 + 3 + 4 = 0 $ (C) 10作为答案。~Baolan

解决方案 3

取首项-10与末项14的平均值，可得该集合的均值为2。每行、每列或对角线均有5个数，因此公共和为 $ 5 \cdot 2 $ ，即10。~Arctic_Bunny，KINGLOGIC 编辑

2020 AMC 10A 试题/第8题

问题

的值是多少

$ 1 + 2 + 3 - 4 + 5 + 6 + 7 - 8 + \cdots + {197} + {198} + {199} - {200}? $

(A) 9,800 (B) 9,900 (C) 10,000 (D) 10,100 (E)10,200

解决方案1

将偶数与奇数分开。若将每两个偶数归为一组并相加，总和为 $ {50} \cdot \left( {-2}\right) = - {100} $ 。对奇数求和等同于对前100个奇数求和，结果为 $ {100}^{2} = {10000} $ 。将两者相加，我们得到答案 $ \left( \mathrm{B}\right) {9900} $ 。

解法2(暴力法)

我们可以把整个求和拆成4个整数位，其中总和为 $ {2x} $ ，而 $ x $ 是该位中的第一个整数。我们发现每个序列的第一个和都是 $ {4x} - 3 $ ，将其代入整个序列的50位得到 $ 1 + 2 + 3 + \cdots + {50} = {1275} $ ，于是可将其代入我们上面得到的每个序列方程的第一项 $ 4\left( {1275}\right) - 3\left( {50}\right) = {4950} $ ，因此每一位的和就是 $ {2x} $ ，而我们只算出了 $ x $ 的值，整个序列的和为 $ {4950} \cdot 2 = \left( B\right) {9900} $ -middletonkids

解决方案3

另一种解决方案是将所有内容相加，再减去不需要的部分。第一步是求解

$ 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + \cdots + {197} + {198} + {199} + {200} $ 为此，我们只需将200与201相乘再除以2，得到20100。下一步是减去带负号的数。这一步实际上得做两次，因为我们既要剔除本不该加的数，又要从问题中再减去它们。接着可见，从4到200以4为步长递增，共有50个数需要减去。为此，可计算50乘51除以2，再乘以4，因为我们按4计数而非按1计数。所得结果为5100，但记住，这一步需重复两次。完成后，我们得到10200。最后，只需计算 $ {20100} - {10200} $ ，最终答案为 $ |\mathrm{\left( B\right) }{9900} $

菲尼亚斯1500

解决方案 4

在此解法中，我们将每4项归为一组。我们的分组应为: $ 1 + 2 + 3 - 4 = 2 $ 、 $ 5 + 6 + 7 - 8\dot{} = {10},9 + {10} + {11} - {12} = {18},\ldots $

$ {197} + {198} + {199} - {200} = {394} $ 。我们将它们相加，得到如下表达式: $ 2 + {10} + {18} + \ldots + {394} $ 。这可以改写为

$ 8 * \left( {0 + 1 + 2 + \ldots + {49}}\right) + {100} $ 我们将其加入get(B9900)。~宝蓝

解决方案 5

我们可以把这个长求和拆成每四个整数一组。先计算前几组的和，得到 $ 1 + 2 + 3 - 4 = 2 $ 、 $ 5 + 6 + 7 - 8 = {10} $ 和 $ 9 + {10} + {11} - {12} = {18} $ 。注意到这是一个递增的等差数列，公差为8。我们可以通过求首项与末项的平均值，再乘以项数，来得到该等差数列的和。首项为 $ 1 + 2 + 3 - 4 $ ，即2；末项为 $ {197} + {198} + {199} - {200} $ ，即394；共有 $ {200} \div 4 $ ，即50项。因此，该数列的和为 $ \frac{\left( {{394} + 2}\right) \cdot {50}}{2} $ ，即(B) 9900。~Arctic_Bunny

2020 AMC 10A 试题/第9题

问题

在学校活动中，一个长凳区段(bench section)可以容纳7名成人或11名儿童。当 $ N $ 个长凳区段首尾相连时，若让相同数量的成人和儿童一起就座，恰好占满所有长凳空间。 $ N $ 的最小可能正整数值是多少？

(A) 9 (B) 18 (C) 27 (D) 36 (E) 77

解决方案

7和11的最小公倍数是77。因此，必须有77名成人和77名儿童。长椅的总数为

$ \frac{77}{7} + \frac{77}{11} = {11} + 7 = {13} $

解决方案 2

这与解法1类似，基本思路相同，但无需计算最小公倍数(LCM)。由于7和11都是质数，它们的最小公倍数必定是其乘积。因此答案为 $ 7 + {11} = $ (B) 18 . PB

2020 AMC 10A 试题/第10题

以下问题同时出现在2020年AMC 12A第7题和2020年AMC 10A第10题，因此两道题均重定向至此。

问题10

七个立方体，其体积分别为1、8、27、64、125、216和343立方单位，垂直堆叠成一座塔，且立方体的体积自下而上递减。除最底部的立方体外，每个立方体的底面都完全位于其下方立方体的顶面上。求这座塔(包括底部)的总表面积，单位为平方单位。

(A) 644 (B) 658 (C) 664 (D) 720 (E) 749

解决方案 1

每个立方体的体积遵循 $ {n}^{3} $ 递增的模式，因为 $ n $ 介于1到7之间。

我们看到总表面积可分为三部分:立方体的侧面、立方体的顶面，以及 $ 7 \times 7 \times 7 $ 立方体的底面(即 $ 7 \times 7 = {49} $ )。侧面积可表示为总和 $ 4\mathop{\sum }\limits_{{n = 0}}^{1}{n}^{2} $ ，得到560。从结构上看，若从顶部观察这座塔，它实际上构成一个 $ 7 \times 7 $ 正方形，面积为49。因此，总表面积为 $ {560} + {49} + {49} = $ (B)658。此外，对于顶面面积，我们也可求和

$ \mathop{\sum }\limits_{{n = 0}}^{6}\left( {{\left( n + 1\right) }^{2} - {n}^{2}}\right) $ ，同样得到49。

~西塞罗尼

解决方案 2

可以迅速看出，这些立方体的边长是从1到7(含)的整数。

首先，我们将计算立方体的总表面积，忽略重叠部分。该值为

\[ 6\left( {{1}^{2} + {2}^{2} + \cdots + {7}^{2}}\right) = 6\mathop{\sum }\limits_{{n = 1}}^{7}{n}^{2} = 6\left( \frac{7\left( {7 + 1}\right) \left( {2 \cdot 7 + 1}\right) }{6}\right) = 7 \cdot 8 \cdot {15} = {840} \]

然后，我们需要减去立方体重叠的部分。在每一对相邻的立方体之间，较小立方体的一个面被完全覆盖，同时较大立方体的一个面也有相同面积被覆盖。

面。因此，立方体重叠部分的总面积等于 $ 2\mathop{\sum }\limits_{{n = 1}}^{6}{n}^{2} = {182} $ 。减去

从总表面积中减去重叠的表面积，我们得到 $ {840} - {182} = 0 $ (B)658。

~绿宝石方块

解法3(比其他方法稍繁琐)

可以看出，使用立方根(cube roots)的立方体边长均为1到7(含)的整数。

只有边长为1和7的立方体在表面积中有5个面，其余立方体均为3个面。此外，由于立方体是堆叠的，我们需要计算每个 $ {n}^{2} $ 与 $ {\left( n - 1\right) }^{2} $ 边长之间的差值，其中 $ n $ 从7到

于是我们得出如下结论:

$ 5\left( {49}\right) + {13} + 4\left( {36}\right) + {11} + 4\left( {25}\right) + 9 + 4\left( {16}\right) + 7 + 4\left( 9\right) + 5 + 4\left( 4\right) + 3 + 5\left( 1\right) $

然后我们将所有这些相加，得到 $ \left( B\right) {658} $

2020 AMC 10A 试题/第11题

以下题目同时出现在2020年AMC 12A第8题和2020年AMC 10A第11题，因此两道题均重定向至此页面。

问题11

以下4040个数字的中位数是多少？

\[ 1,2,3,\ldots ,{2020},{1}^{2},{2}^{2},{3}^{2},\ldots ,{2020}^{2} \]

我们可以看到 $ {44}^{2} $ 小于2020。因此，在2020之后有1976个4040个数。同时，小于或等于2020的数有2064个。由于 $ {44}^{2} $ 等于1936，它与其他平方数一起将我们的中位数位置向上移动44。我们可以得出整个集合的中位数是2020.5，而 $ {2020.5} - {44} $ 给出1976.5。我们的答案是 $ \left| {\mathbf{\left( C\right) }\;{1976.5}}\right| $

~aryam

解法2

由于我们要找的是一个含4040项的集合的中位数，因此必须求出第2020项与第2021项的平均值。

因为 $ {45}^{2} = {2025} $ 略大于2020，可知44个完全平方数 $ {1}^{2} $ 到 $ {44}^{2} $ 小于2020，其余均大于2020。于是，从数字1到2020共有 $ {2020} + {44} = {2064} $ 项。由于 $ {44}^{2} $ 比 $ {45}^{2} = {2025} $ 小 $ {44} + {45} = {89} $ ，且比2020小84，我们只需从第2064项2020开始向下数84项，再考虑完全平方项即可。第2020项与第2021项距第2064项分别只有44项和43项，因此只需从2020中减去44和43，即得1976与1977。取二者平均，得到

解法3

我们需要知道第2020项和第2021项，以求中位数。

我们知道 $ {44}^{2} = {1936} $

因此数字 $ {1}^{2},{2}^{2},...,{44}^{2} $ 位于1到1936之间。

于是44与1936之和为1980，这意味着1936是第1980个数。

同时注意到 $ {45}^{2} = {2025} $ ，它大于2021。

因此第2020项为 $ {1936} + {40} = {1976} $ ，同理第2021项为1977

求这两个数的中位数，得到(C,1976.5)

~toastybaker

2020 AMC 10A 试题/第12题

题目

三角形 $ {AMC} $ 是等腰三角形，且 $ {AM} = {AC} $ 。中线 $ \overline{MV} $ 与 $ \overline{CU} $ 互相垂直，且 $ {MV} = {CU} = {12} $ 。求 $ \bigtriangleup {AMC} $ 的面积？

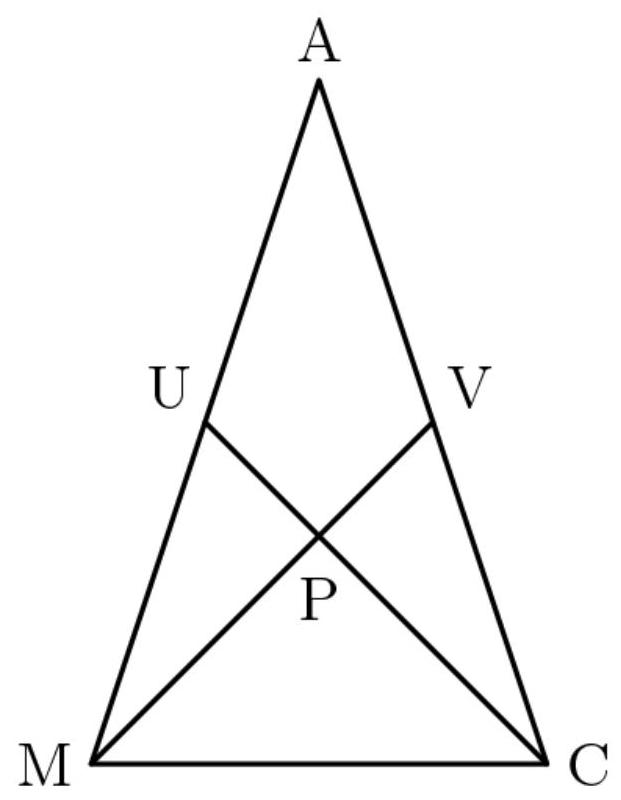
(A) 48 (B) 72 (C) 96 (D) 144 (E) 192 解法1

由于四边形 $ {UVCM} $ 的对角线互相垂直，其面积等于对角线长度乘积的一半。又注意到 $ \bigtriangleup {AUV} $ 与三角形 $ {AMC} $ 相似，面积比为 $ \frac{1}{4} $ ，因此 $ \left\lbrack {UVCM}\right\rbrack = \frac{3}{4} \cdot \left\lbrack {AMC}\right\rbrack $ 。于是，

\[ \frac{1}{2} \cdot {12} \cdot {12} = \frac{3}{4} \cdot \left\lbrack {AMC}\right\rbrack \]

\[ {72} = \frac{3}{4} \cdot \left\lbrack {AMC}\right\rbrack \]

\[ \left\lbrack {AMC}\right\rbrack = {96} \rightarrow \left( \mathbf{C}\right) . \]

解法2(梯形)我们知道 $ \bigtriangleup {AUV} \sim \bigtriangleup {AMC} $ ，且其边长比为 $ \frac{1}{2} $ ，故面积比为 $ {\left( \frac{1}{2}\right) }^{2} = \frac{1}{4} $ 。

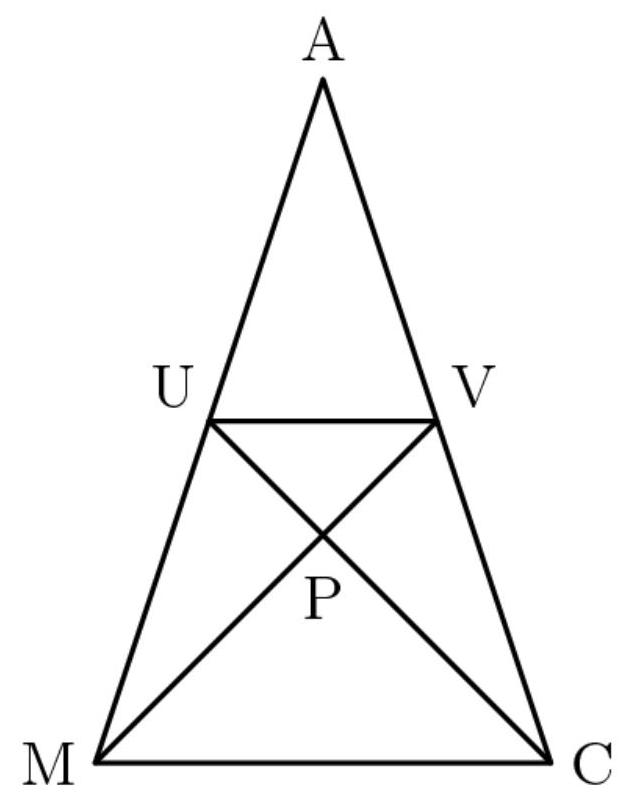
若 $ \bigtriangleup {AUV} $ 是 $ \bigtriangleup {AMC} $ 面积的 $ \frac{1}{4} $ ，则梯形 $ {MUVC} $ 是 $ \bigtriangleup {AMC} $ 面积的 $ \frac{3}{4} $ 。

设 $ \overline{UC} $ 与 $ \overline{MV}P $ 的交点为。令 $ \overline{UP} = x $ 。则 $ \overline{PC} = {12} - x $ 。由于 $ \overline{UC} \bot \overline{MV} $ ， $ \overline{UP} $ 与 $ \overline{CP} $ 分别是三角形 $ \bigtriangleup {MUV} $ 和 $ \bigtriangleup {MCV} $ 的高，这两个三角形的底均为12。

$ \bigtriangleup {MUV} = \frac{x \cdot {12}}{2} = {6x} $ 的面积

$ \bigtriangleup {MCV} = \frac{\left( {{12} - x}\right) \cdot {12}}{2} = {72} - {6x} $ 的面积

将两者相加得到梯形 $ {MUVC} $ 的面积，即 $ {6x} + \left( {{72} - {6x}}\right) = {72}. $

这是三角形面积的 $ \frac{3}{4} $ ，因此三角形面积为 $ \frac{4}{3} \cdot {72} = $ (C) 96 ~quacker88，图由programjames1绘制

解法3(中线)

作中线 $ \overline{AB} $ 。

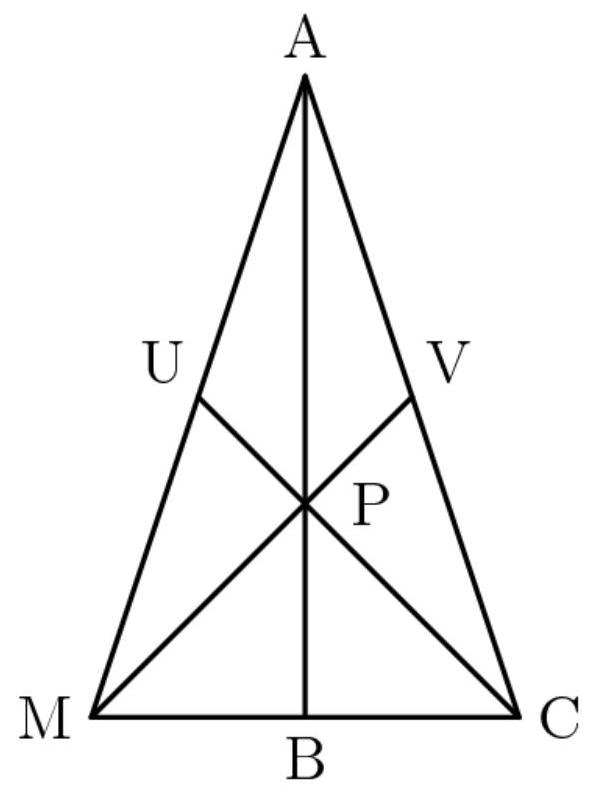
由于三角形所有中线交于重心，可知 $ \overline{AB} $ 经过点 $ P $ 。又知中线将彼此分成 $ 2 : 1 $ 的比例，由此可得 $ \overline{PC} $ 。 $ \overline{UP} = 2 : 1 $ ，且两段之和为12，故 $ \overline{PC} $ 与 $ \overline{UP} $ 分别为8和4。

最后，由于中线将三角形分成6个面积相等的部分，只需计算 $ \bigtriangleup {PUM} $ 的面积即可。 $ \overline{PC} = \overline{MP} = 8 $ 。

$ \bigtriangleup {PUM} = \frac{4 \cdot 8}{2} = {16} $ 的面积为。乘以6得

$ 6 \cdot {16} = \left( {\mathbf{C}\mathbf{C}}\right) {96} $

~quacker88

解法4(三角形)

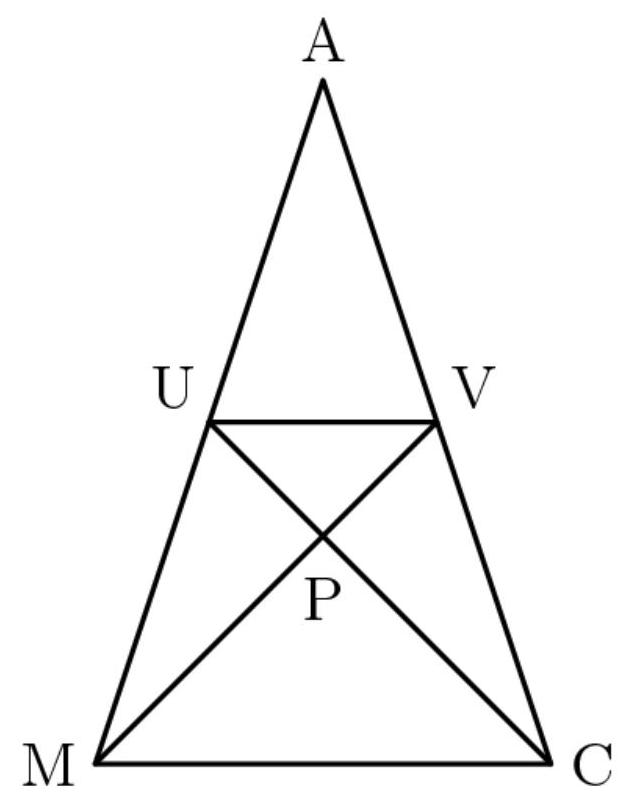
我们知道 $ {AU} = {UM},{AV} = {VC}, $ ，因此 $ {UV} = \frac{1}{2}{MC} $ 。

由于 $ \angle {UPM} = \angle {VPC} = {90} $ ，我们可以看出 $ \bigtriangleup {UPM} \cong \bigtriangleup {VPC} $ 和 $ \bigtriangleup {UVP} \sim \bigtriangleup {MPC} $ ，其边长比为 $ 1 : 2 $ 。

\[ \text{So}{UP} = {VP} = 4\text{,}{MP} = {PC} = 8\text{.} \]

由此可知 $ S{\bigtriangleup {UPM}} = {16} $ ，梯形 $ M{UVC} $ 的面积为72。

如解法1所述， $ S\bigtriangleup {AMC} = {72}/\frac{3}{4} = $ (C)96

-QuadraticFunctions，解法1作者不详

解法5(仅用勾股定理)

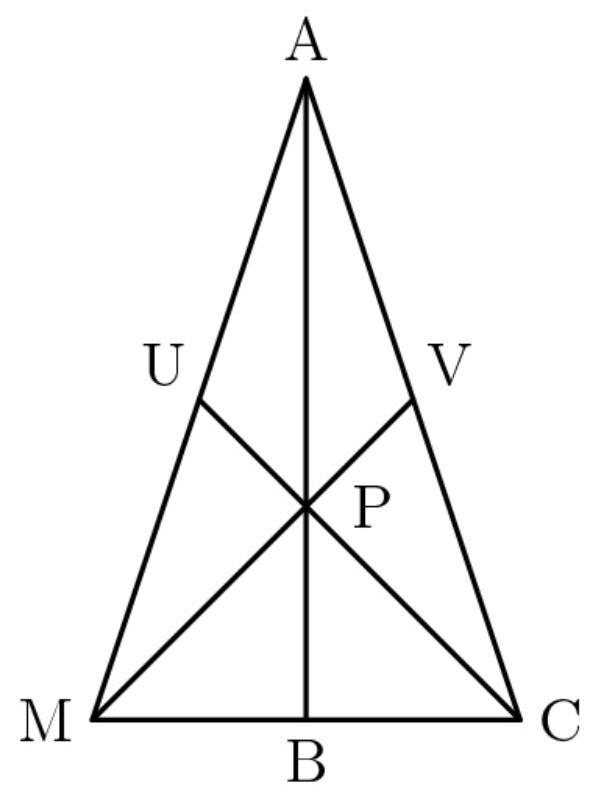
设 $ {AB} $ 为高。由于中线互相分成 $ 2 : 1 $ 的比例，且中线长度为12，我们有 $ {PC} = {MP} = 8 $ 和 $ {UP} = {UV} = 4 $ 。从直角三角形 $ \bigtriangleup {MUP} $ ，

\[ M{U}^{2} = M{P}^{2} + U{P}^{2} = {8}^{2} + {4}^{2} = {80}, \]

因此 $ {MU} = \sqrt{80} = 4\sqrt{5} $ 。由于 $ {CU} $ 是中线， $ {AM} = 8\sqrt{5} $ 。从直角三角形 $ \bigtriangleup {MPC} $ ，

\[ M{C}^{2} = M{P}^{2} + P{C}^{2} = {8}^{2} + {8}^{2} = {128}, \]

这意味着 $ {MC} = \sqrt{128} = 8\sqrt{2} $ 。根据对称性

\[ {MB} = \frac{8\sqrt{2}}{2} = 4\sqrt{2}. \]

对直角三角形 $ \bigtriangleup {MAB} $ 应用勾股定理，得到

\[ A{B}^{2} = A{M}^{2} - M{B}^{2} = 8{\sqrt{5}}^{2} - 4{\sqrt{2}}^{2} = {288}\text{, so} \]

$ {AB} = \sqrt{288} = {12}\sqrt{2} $ 。那么 $ \bigtriangleup {AMC} $ 的面积为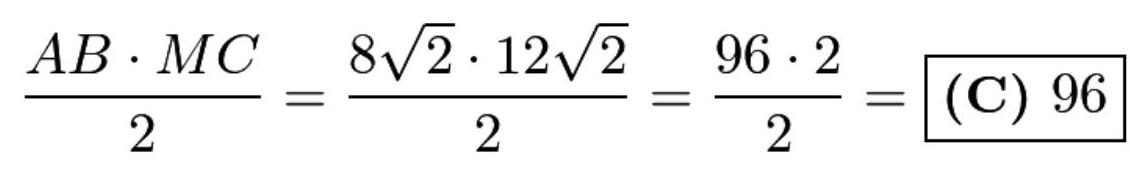

解法6(作图法)

(不推荐)将给出的图形(恰好是按比例绘制的)转绘到方格纸上。由于选项差距较大，数格子应能得到可靠结果。-Lingjun

解法7

给定一个三角形，其两条中线互相垂直，长度分别为 $ x $ 和 $ y $ ，则面积为 $ \frac{2xy}{3} = $ (C)96

解法8(最快)

连接线段 $ {UV} $ ，很容易看出四边形 $ {UVMC} $ 的面积为对角线乘积的一半，即72。现在，求解三角形 $ A{UV} $ 的面积是一个选择，但图示表明 $ A{UV} $ 的面积小于四边形，这意味着 $ {AMC} $ 的面积小于 $ {72} * 2 $ 但大于72，因此唯一可能的选项是 $ \left( {\mathrm{C}\text{)}{96}}\right) $ 。

2020 AMC 10A 试题/第13题

问题13

一只青蛙从点(1,2)出发，开始一系列跳跃，每次跳跃平行于坐标轴之一，长度为1，且每次跳跃的方向(上、下、右或左)独立随机选择。当青蛙到达以 $ \left( {0,0}\right) ,\left( {0,4}\right) ,\left( {4,4}\right) , $ 和(4,0)为顶点的正方形的一条边时，序列结束。求跳跃序列在正方形的垂直边上结束的概率。

(A) $ \frac{1}{2} $ (B) $ \frac{5}{8} $ (C) $ \frac{2}{3} $ (D) $ \frac{3}{4} $ (E) $ \frac{7}{8} $

解决方案

画出正方形后很容易看出，如果青蛙向左跳，它会立刻碰到正方形的竖直边界，因此这种情况发生的概率是 $ \frac{1}{4} * 1 = \frac{1}{4} $ 。如果青蛙向右跳，它会到达正方形中心(2,2)；由于对称性(青蛙到正方形各边的距离相等)，它碰到正方形竖直边的概率是 $ \frac{1}{2} $ ，这种情况发生的概率为 $ \frac{1}{4} * \frac{1}{2} = \frac{1}{8} $ 。

如果青蛙向上或向下移动，它将撞向离它最近和最远的角落所形成的对称线，并且它到两条较近边的距离相等，到两条较远边的距离也相等。它撞向垂直墙的概率为 $ \frac{1}{2} $ 。由于青蛙向上或向下移动的概率为 $ \frac{1}{2} $ ，因此该情况的总概率为 $ \frac{1}{2} * \frac{1}{2} = \frac{1}{4} $ ，将所有情况相加，

\[ \frac{1}{4} + \frac{1}{8} + \frac{1}{4} = \frac{5}{8} \Rightarrow \text{ (B) }\frac{5}{8}. \]

解决方案 2

假设我们有一个4×4的网格，我们用分类讨论的方法来解决这个问题。A是青蛙的初始位置，B和C是第二次跳跃可能到达的位置，O代表其他所有格子。如果我们落在C，就表示到达了竖直边；如果落在B，由于我们处于对称位置，到达水平边和竖直边的概率相等。因此，落在C的概率是 $ 1/4 $ ，落在B的概率是 $ 3/4 $ 。由于C代表“成功”，而B意味着有一半的成功机会，我们计算 $ 1 \cdot C + \frac{1}{2} \cdot B $ 。

\[ 1 \cdot \frac{1}{4} + \frac{1}{2} \cdot \frac{3}{4} \]

\[ \frac{1}{4} + \frac{3}{8} \]

我们得到 $ \frac{5}{8} $ ，或者 $ B $

\[ \text{O O O O O} \]

O B O O O

\[ \text{C A B O O} \]

O B O O O O O O O O

-是的

解决方案 3

如果青蛙位于两条对角线之一，落在垂直或水平方向的概率均变为 $ \frac{1}{2} $ 。由于它从(1,2)出发，第一次跳跃有 $ \frac{3}{4} $ 的概率(向上、向下或向右)到达对角线，有 $ \frac{1}{4} $ 的概率(向左)到达垂直边。落在垂直方向的概率为 $ \frac{1}{4} + \frac{3}{4} * \frac{1}{2} = 0 $ (B) $ \frac{5}{8} $ 。Lingjun

解法4(完整状态)

令 $ {P}_{\left( x, y\right) } $ 表示青蛙位于(x, y)时，其跳跃序列以碰到竖直边结束的概率。注意，根据关于直线 $ x = 2 $ 的反射对称性， $ {P}_{\left( 1,2\right) } = {P}_{\left( 3,2\right) } $ 。类似地， $ {P}_{\left( 1,1\right) } = {P}_{\left( 1,3\right) } = {P}_{\left( 3,1\right) } = {P}_{\left( 3,3\right) } $ ，且 $ {P}_{\left( 2,1\right) } = {P}_{\left( 2,3\right) } $ 。现在，我们通过考虑从该点向上、下、左、右移动的概率，为这些点/状态的概率建立方程:

\[ {P}_{\left( 1,2\right) } = \frac{1}{4} + \frac{1}{2}{P}_{\left( 1,1\right) } + \frac{1}{4}{P}_{\left( 2,2\right) } \]

\[ {P}_{\left( 2,2\right) } = \frac{1}{2}{P}_{\left( 1,2\right) } + \frac{1}{2}{P}_{\left( 2,1\right) } \]

\[ {P}_{\left( 1,1\right) } = \frac{1}{4} + \frac{1}{4}{P}_{\left( 1,2\right) } + \frac{1}{4}{P}_{\left( 2,1\right) } \]

\[ {P}_{\left( 2,1\right) } = \frac{1}{2}{P}_{\left( 1,1\right) } + \frac{1}{4}{P}_{\left( 2,2\right) } \]

我们得到一个含4个变量的4方程组，因此可以解出这些概率。将第二个方程代入第四个方程得

\[ {P}_{\left( 2,1\right) } = \frac{1}{2}{P}_{\left( 1,1\right) } + \frac{1}{4}\left( {\frac{1}{2}{P}_{\left( 1,2\right) } + \frac{1}{2}{P}_{\left( 2,1\right) }}\right) \]

\[ {P}_{\left( 2,1\right) } = \frac{8}{7}\left( {\frac{1}{2}{P}_{\left( 1,1\right) } + \frac{1}{8}{P}_{\left( 1,2\right) }}\right) = \frac{4}{7}{P}_{\left( 1,1\right) } + \frac{1}{7}{P}_{\left( 1,2\right) } \]

再将第三个方程代入上式得

\[ {P}_{\left( 2,1\right) } = \frac{4}{7}\left( {\frac{1}{4} + \frac{1}{4}{P}_{\left( 1,2\right) } + \frac{1}{4}{P}_{\left( 2,1\right) }}\right) + \frac{1}{7}{P}_{\left( 1,2\right) } \]

\[ {P}_{\left( 2,1\right) } = \frac{7}{6}\left( {\frac{1}{7} + \frac{2}{7}{P}_{\left( 1,2\right) }}\right) = \frac{1}{6} + \frac{1}{3}{P}_{\left( 1,2\right) }\left( *\right) \]

(*)

接着，将第二和第三个方程代入第一个方程得

\[ {P}_{\left( 1,2\right) } = \frac{1}{4} + \frac{1}{2}\left( {\frac{1}{4} + \frac{1}{4}{P}_{\left( 1,2\right) } + \frac{1}{4}{P}_{\left( 2,1\right) }}\right) + \frac{1}{4}\left( {\frac{1}{2}{P}_{\left( 1,2\right) } + \frac{1}{2}{P}_{\left( 2,1\right) }}\right) \]

\[ {P}_{\left( 1,2\right) } = \frac{3}{8} + \frac{1}{4}{P}_{\left( 1,2\right) } + \frac{1}{4}{P}_{\left( 2,1\right) } \]

现在将(*)代入上式，我们得到

\[ {P}_{\left( 1,2\right) } = \frac{3}{8} + \frac{1}{4}{P}_{\left( 1,2\right) } + \frac{1}{4}\left( {\frac{1}{6} + \frac{1}{3}{P}_{\left( 1,2\right) }}\right) \]

\[ {P}_{\left( 1,2\right) } = \frac{3}{2} \cdot \frac{5}{12} = 6\mathrm{\;B}2\frac{5}{8} \]

2020 AMC 10A 第14题

实数 $ x $ 和 $ y $ 满足 $ x + y = 4 $ 和 $ x \cdot y = - 2 $ 。求

\[ x + \frac{{x}^{3}}{{y}^{2}} + \frac{{y}^{3}}{{x}^{2}} + y? \]

(A) 360 (B) 400 (D) 440 (E) 480

注:所有解法均涉及因式分解

解法1

\[ x + \frac{{x}^{3}}{{y}^{2}} + \frac{{y}^{3}}{{x}^{2}} + y = x + \frac{{x}^{3}}{{y}^{2}} + y + \frac{{y}^{3}}{{x}^{2}} = \frac{{x}^{3}}{{x}^{2}} + \frac{{y}^{3}}{{x}^{2}} + \frac{{y}^{3}}{{y}^{2}} + \frac{{x}^{3}}{{y}^{2}} \]

继续合并

\[ \frac{{x}^{3} + {y}^{3}}{{x}^{2}} + \frac{{x}^{3} + {y}^{3}}{{y}^{2}} = \frac{\left( {{x}^{2} + {y}^{2}}\right) \left( {{x}^{3} + {y}^{3}}\right) }{{x}^{2}{y}^{2}} = \frac{\left( {{x}^{2} + {y}^{2}}\right) \left( {x + y}\right) \left( {{x}^{2} - {xy} + {y}^{2}}\right) }{{x}^{2}{y}^{2}} \]

由已知可得 $ {x}^{2}{y}^{2} = 4 $ 。同时，

\[ {\left( x + y\right) }^{2} = {x}^{2} + {2xy} + {y}^{2} = {16} \]

这意味着 $ {x}^{2} + {y}^{2} = {20} $ 。将此信息代入

$ \frac{\left( {{x}^{2} + {y}^{2}}\right) \left( {x + y}\right) \left( {{x}^{2} - {xy} + {y}^{2}}\right) }{{x}^{2}{y}^{2}} $ ，我们有

$ \frac{\left( {20}\right) \left( 4\right) \left( {22}\right) }{4} = {20} \cdot {22} = {(D)440}. \sim $ PCChess

解法2

如上所述，我们需要计算 $ \frac{\left( {{x}^{2} + {y}^{2}}\right) \left( {{x}^{3} + {y}^{3}}\right) }{{x}^{2}{y}^{2}} $ 。注意 $ x, y $ 是 $ {x}^{2} - {4x} - 2 $ 的根，因此 $ {x}^{3} = 4{x}^{2} + {2x} $ 且 $ {y}^{3} = 4{y}^{2} + {2y} $ 。于是 $ {x}^{3} + {y}^{3} = 4\left( {{x}^{2} + {y}^{2}}\right) + 2\left( {x + y}\right) = 4\left( {20}\right) + 2\left( 4\right) = {88} $ ，其中 $ {x}^{2} + {y}^{2} = {20} $ 和 $ {x}^{2}{y}^{2} = 4 $ 与前一解法相同。因此答案为 $ \frac{\left( {20}\right) \left( {88}\right) }{4} = $ (D)440。

Emathmaster

解法3

注意 $ \left( {{x}^{3} + {y}^{3}}\right) \left( {\frac{1}{{y}^{2}} + \frac{1}{{x}^{2}}}\right) = x + \frac{{x}^{3}}{{y}^{2}} + \frac{{y}^{3}}{{x}^{2}} + y $ 。现在，我们只需找出 $ {x}^{3} + {y}^{3} $ 和 $ \frac{1}{{y}^{2}} + \frac{1}{{x}^{2}} $ 的值。

回忆 $ {x}^{3} + {y}^{3} = \left( {x + y}\right) \left( {{x}^{2} - {xy} + {y}^{2}}\right) , $ 且 $ {x}^{2} - {xy} + {y}^{2} = {\left( x + y\right) }^{2} - {3xy}. $ 。我们可以解第二个方程，解得 $ {4}^{2} - 3\left( {-2}\right) = {22}. $ 。将其代入第一个方程，得到 $ {x}^{3} + {y}^{3} = 4\left( {22}\right) = {88} $ 。

为了求 $ \frac{1}{{y}^{2}} + \frac{1}{{x}^{2}} $ 的值，我们通分以便相加，得到 $ \frac{{x}^{2}}{{x}^{2}{y}^{2}} + \frac{{y}^{2}}{{x}^{2}{y}^{2}} = \frac{{x}^{2} + {y}^{2}}{{\left( xy\right) }^{2}} $ 。回忆 $ {x}^{2} + {y}^{2} = {\left( x + y\right) }^{2} - {2xy} $ 并解此方程，得 $ {4}^{2} - 2\left( {-2}\right) = {20}. $ 。将其代入第一个方程，得到

\[ \frac{1}{{y}^{2}} + \frac{1}{{x}^{2}} = \frac{20}{{\left( -2\right) }^{2}} = 5. \]

解原方程，得

$ x + \frac{{x}^{3}}{{y}^{2}} + \frac{{y}^{3}}{{x}^{2}} + y = \left( {88}\right) \left( 5\right) = $ (D) 440.

解法4

这基本上是用韦达公式(Vieta’s formulas)硬算 $ x $ 和 $ y $ (我极不推荐，只是写着玩)。

我们利用韦达定理(Vieta’s)建立与 $ x $ 和 $ y $ 相关的二次方程。令 $ x $ 和 $ y $ 为二次方程 $ Q\left( n\right) = {n}^{2} - {4n} - 2 $ 的根(因为 $ x + y = 4 $ ，且 $ {xy} = - 2 $ )。解该二次方程可得根 $ 2 + \sqrt{6} $ 和 $ 2 - \sqrt{6} $ 。 $ x $ 与 $ y $ “可互换”，即无论 $ x $ 或 $ y $ 取哪个解，代入后结果相同。于是我们将 $ 2 + \sqrt{6} $ 代入 $ x $ ， $ 2 - \sqrt{6} $ 代入 $ y $ ，得到答案 $ \left| {\left( \mathrm{D}\right) {440}}\right| $ 。

~Baolan

视频解析

https://youtu.be/ZGwAasE32Y4

~lceMatrix 另见

2020 AMC 10A 第15题

题目

从 $ {12}! $ 的正整数因子中随机选取一个。选出的因子是完全平方数的概率可表示为 $ \frac{m}{n} $ ，其中 $ m $ 与 $ n $ 为互质的正整数。 $ m + n $ 是多少？

(A) 3 (B) 5 (C) 12 (D) 18 (E) 23 解答

$ {12}! $ 的质因数分解为 $ {2}^{10} \cdot {3}^{5} \cdot {5}^{2} \cdot 7 \cdot {11} $ ，因此共有 $ {11} \cdot 6 \cdot 3 \cdot 2 \cdot 2 $ 个因子。要得到完全平方因子，每个质因数的指数必须为偶数。注意7和11不能出现在完全平方因子的质因数分解中，因为 $ {12}!. $ 中各仅出现一次。于是共有 $ 6 \cdot 3 \cdot 2 $ 个完全平方数。(对于2，指数可取0、2、4、6、8或10，等等。)选出的因子为完全平方数的概率为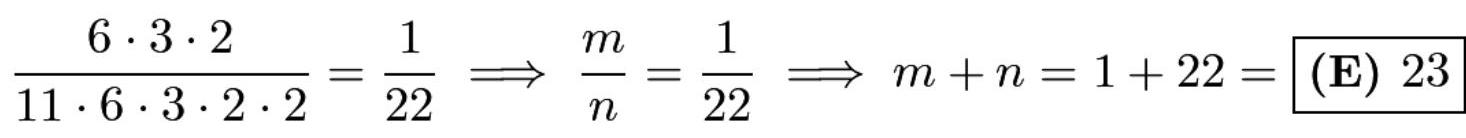~mshell214，由Rzhpamath编辑

视频解析

https://youtu.be/ZGwAasE32Y4

~lceMatrix 另见

2020 AMC 10A 第16题

以下题目同时出现在2020 AMC 12A第16题和2020 AMC 10A第16题，因此两题均重定向至此页面。

题目

在坐标平面上，顶点为 $ \left( {0,0}\right) ,\left( {{2020},0}\right) ,\left( {{2020},{2020}}\right) , $ 和(0,2020)的正方形内随机取一点。该点与某个格点距离不超过 $ d $ 的概率为 $ \frac{1}{2} $ 。(若 $ x $ 与 $ y $ 均为整数，则点(x, y)为格点。) $ d $ 四舍五入到小数点后一位是多少？

(A)0.3(B)0.4(C)0.5(D)0.6(E)0.7

解法1

图示

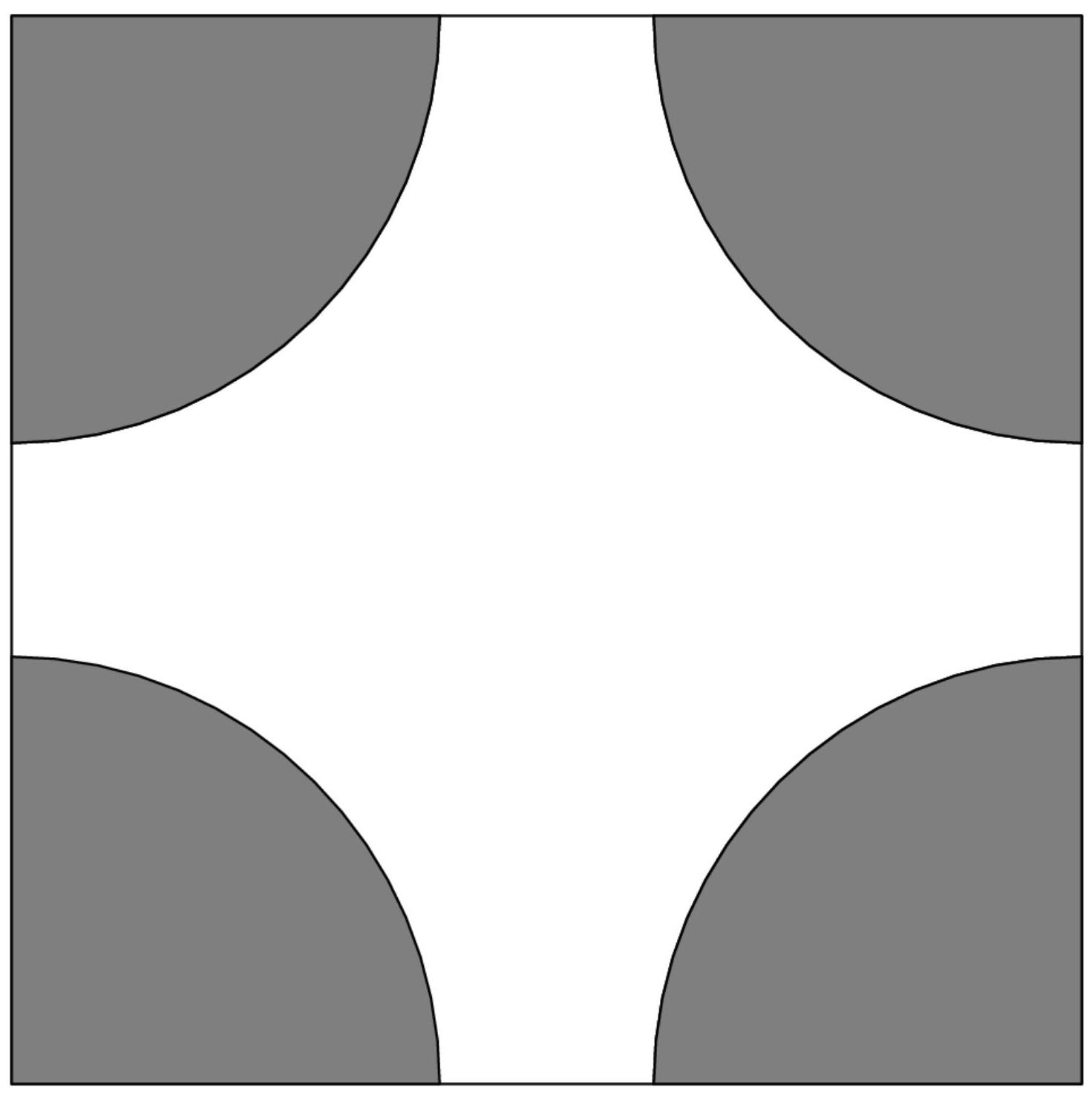
由Shurong.ge使用Asymptote绘制的图示

注:该图示表示给定 $ {2020} * {2020} $ 正方形的每个单位方格。

解法

我们考虑一个1×1的独立方块。

若从每个角(格点所在位置)画一个半径为 $ d $ 的四分之一圆，则这些圆覆盖的面积应为0.5。因此，考虑到共有四个圆，我们列出

\[ 4 * \frac{1}{4} * \pi {d}^{2} = \frac{1}{2} \]

解 $ d $ ，得 $ d = \frac{1}{\sqrt{2\pi }} $ ，其中当 $ \pi \approx 3 $ 时，我们得到 $ d = \frac{1}{\sqrt{6}} $ ，由此化简可见 $ d \approx {0.4} \Rightarrow d $ (B)0.4。 $ \sim $ Crypthes

$ \mathbf{{Note} : } $ 为更严谨，注意 $ d < {0.5} $ ，因为若 $ d \geq {0.5} $ ，则概率显然大于 $ \frac{1}{2} $ 。这确保上述解法成立，因为若 $ d \geq {0.5} $ ，四分之一圆会重叠。—— $ \mathbf{{Emathmaster}} $

解法2

与前一解法相同，我们得到方程 $ 4 * \frac{1}{4} * \pi {d}^{2} = \frac{1}{2} $ ，化简为 $ \pi {d}^{2} = \frac{1}{2} = {0.5} $ 。由于 $ \pi $ 略大于3， $ {d}^{2} $ 略小于 $ \frac{0.5}{3} = {0.1}\overline{6} $ 。我们注意到 $ {0.1}\overline{6} $ 略大于 $ {0.4}^{2} = {0.16} $ ，因此 $ d $ 约为 $ \left( {B){0.4}}\right) $ 。——emerald_block

解法3(估算)

如上，我们需估算 $ d = \frac{1}{\sqrt{2\pi }} $ 。

注意我们可近似 $ {2\pi } \approx {6.28} \approx {6.25} $ ，于是 $ \frac{1}{\sqrt{2\pi }} $

$ \approx \frac{1}{\sqrt{6.25}} = \frac{1}{2.5} = {0.4}. $

因此答案为 $ \begin{array}{l} \text{ (B) }{0.4} \end{array} $

~银龙

2020 AMC 10A 试题/第17题

定义

\[ P\left( x\right) = \left( {x - {1}^{2}}\right) \left( {x - {2}^{2}}\right) \cdots \left( {x - {100}^{2}}\right) . \]

有多少个整数 $ n $ 满足 $ P\left( n\right) \leq 0 $ ？

(A) 4900 (B) 4950 (C) 5000 (D) 5050 (E) 5100

解决方案 1

注意 $ P\left( x\right) $ 是许多整数的乘积。我们需要其中一个因子为0，或者有奇数个负因子。

案例1:存在100个整数 $ n $ ，使得 $ P\left( x\right) = 0 $

情况2:要使负因数的个数为奇数， $ n $ 必须介于一个奇数的平方与一个偶数的平方之间。这意味着 $ n $ 共有 $ 2 + 6 + \cdots + {198} $ 个可能的取值。化简后，共有5000个可能的数。

综上所述， $ n $ 共有(E,5100)种可能的取值。PCChess

解决方案 2

注意到当 $ x $ 介于 $ {100}^{2} $ 与 $ {99}^{2} $ 、 $ {98}^{2} $ 与 $ {97}^{2}\ldots $ 、 $ {2}^{2} $ 与 $ {1}^{2} $ 之间(含端点)时， $ P\left( x\right) $ 为非正，这意味着数值的数量等于

$ \left( {\left( {{100} + {99}}\right) \left( {{100} - {99}}\right) + 1}\right) + \left( {\left( {{98} + {97}}\right) \left( {{98} - {97}}\right) + 1}\right) + \ldots + \left( {\left( {2 + 1}\right) \left( {2 - 1}\right) + 1}\right) $

这简化为

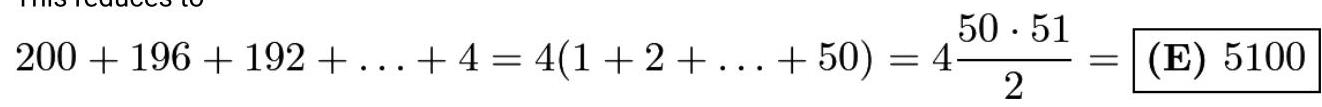
~泽里克

解法3(末端行为)

我们知道 $ P\left( x\right) $ 是一个100次函数(100-degree function)，且其首项系数为正。也就是说， $ P\left( x\right) = {x}^{100} + a{x}^{99} + b{x}^{98} + \ldots + $ (常数)。由于 $ P\left( x\right) $ 的次数为偶数，其两端的行为一致；又因为首项系数为正，所以当 $ x $ 向任意方向趋近时，两端都趋近于 $ \infty $ 。

\[ \mathop{\lim }\limits_{{x \rightarrow - \infty }}P\left( x\right) = \mathop{\lim }\limits_{{x \rightarrow \infty }}P\left( x\right) = \infty \]

因此， $ P\left( x\right) $ 第一次为负是在它与 $ x $ 轴相交于一个 $ x $ 截距并向下穿过时。这发生在 $ {1}^{2} $ ，即最小的截距处。

然而，当它到达下一个截距时，又会回升到正值区域，我们知道这发生在 $ {2}^{2} $ 。而当它到达 $ {3}^{2} $ 时，又会再次跌入负值区域。显然，这一过程将沿着截距不断“蛇形”前进，直到 $ {100}^{2} $ 。

要计算位于 $ x $ 轴下方或轴上的整数个数，我们只需数整数即可。例如，对于之前得到的 $ \left\lbrack {{1}^{2},{2}^{2}}\right\rbrack $ 区间内的整数个数，我们减一、加一。 $ \left( {{2}^{2} - {1}^{2} + 1}\right) = 4 $ 个整数，因此该区间内有四个整数使结果为负。

对所有其他区间重复此操作，我们得到

$ \left( {{2}^{2} - {1}^{2} + 1}\right) + \left( {{4}^{2} - {3}^{2} + 1}\right) + \ldots + \left( {{100}^{2} - {99}^{2} + 1}\right) $ 。继续采用解法2。~quacker88

2020 AMC 10A 试题/第18题

题目

设(a, b, c, d)为一个有序四元组，其中元素不必互异，每个元素取自集合{0,1,2,3}。有多少个这样的四元组满足 $ a \cdot d - b \cdot c $ 为奇数？(例如，(0,3,1,1)就是一个这样的四元组，因为 $ 0 \cdot 1 - 3 \cdot 1 = - 3 $ 为奇数。)

(A) 48 (B) 64 (C) 96 (D) 128 (E) 192

解答

解法1(奇偶性)

为了使 $ a \cdot d - b \cdot c $ 为奇数，考虑奇偶性。我们必须有(偶数)-(奇数)或(奇数)-(偶数)。有 $ 2 \cdot 4 + 2 \cdot 2 = {12} $ 种方式选取数字以得到偶数积。有 $ 2 \cdot 2 = 4 $ 种方式得到奇数积。因此，

使 $ a \cdot d - b \cdot c $ 为奇数的总方式数为 $ 2 \cdot \left( {{12} \cdot 4}\right) = \left( \mathbf{C}\right) {96} $

-Midnight

解法2(本质上是解法1，但更详细)

考虑奇偶性。我们需要恰好一项为奇数，一项为偶数。由于对称性，可设 $ {ad} $ 为奇数， $ {bc} $ 为偶数，然后乘以2。若 $ {ad} $ 为奇数，则 $ a $ 和 $ d $ 必须均为奇数，因此 $ {ad}. $ 有 $ 2 \cdot 2 = 4 $ 种可能。考虑 $ {bc}. $ ，设 $ b $ 为偶数，则 $ {bc}. $ 有 $ 2 \cdot 4 = 8 $ 种可能。然而， $ b $ 也可为奇数，此时 $ {bc}. $ 又有 $ 2 \cdot 2 = 4 $ 种可能。因此，选择 $ {bc} $ 有12种方式，选择 $ {ad}. $ 有4种方式。于是，考虑对称性后， $ {ad} - {bc}.\left( C\right) $ 共有 $ 2 * 4 * {12} = {96} $ 个取值。

解法3(补集计数)

独立选择任意数字有4种方式，独立选择任意奇数有2种方式。为了得到偶数积，我们计数:

$ \mathrm{P} $ (任意数字) $ \cdot \mathrm{P} $ (任意数字) $ - \mathrm{P}\left( \mathrm{{odd}}\right) \cdot \mathrm{P}\left( \mathrm{{odd}}\right) $ ，即 $ 4 \cdot 4 - 2 \cdot 2 = {12} $ 。得到奇数积的方式可以这样计数: $ \mathrm{P}\left( \mathrm{{odd}}\right) \cdot \mathrm{P}\left( \mathrm{{odd}}\right) $ ，即 $ 2 \cdot 2 $ ，或4。因此，一个积为奇数另一个为偶数: $ 2 \cdot 4 \cdot {12} = O\left( C\right) {96} $ (顺序重要)。 $ \sim $ Anonymous 和 Arctic_Bunny

解法4(解法3的深入版)

我们使用补集计数:若差为偶数，则可减去这些情况。总共有 $ {4}^{4} = {256} $ 种情况。

对于偶数差，我们有(偶)-(偶)或(奇-奇)。

根据解法3:

“独立选择任意数字有4种方式，独立选择任意奇数有2种方式。偶数积:(数字)×(数字)-(奇数)×(奇数): $ 4 \cdot 4 - 2 \cdot 2 = {12} $ 。奇数积:(奇数)×(奇数): $ 2 \cdot 2 = 4 $ 。”

由此，我们轻松算出 $ {256} - {12}^{2} - {4}^{2} = \mathbf{\left( C\right) {96}} $ 。~kevinmathz

在计算偶数积和奇数积的数量时，由于唯一得到奇数积的方式是将两个奇整数相乘，且有2个奇整数，可迅速推出奇数积有 $ 2 \cdot 2 = 4 $ 种可能。

由于积只能是奇数或偶数，且选择积的因数有 $ 4 \cdot 4 = {16} $ 种方式，因此偶数积有 $ {16} - 4 = {12} $ 种可能。~emerald_block

2020 AMC 10A 问题/第19题

题目

如下图所示，一个正十二面体(由12个全等的正五边形面组成的多面体)在太空中漂浮，有两个水平面。注意，与顶面相邻有一圈五个倾斜面，与底面相邻也有一圈五个倾斜面。有多少种方式可以从顶面出发，通过一系列相邻面移动到顶面，使得每个面最多被访问一次，且不允许从底环移动到顶环？

(A) 125 (B) 250 (C) 405 (D) 640 (E) 810

图示

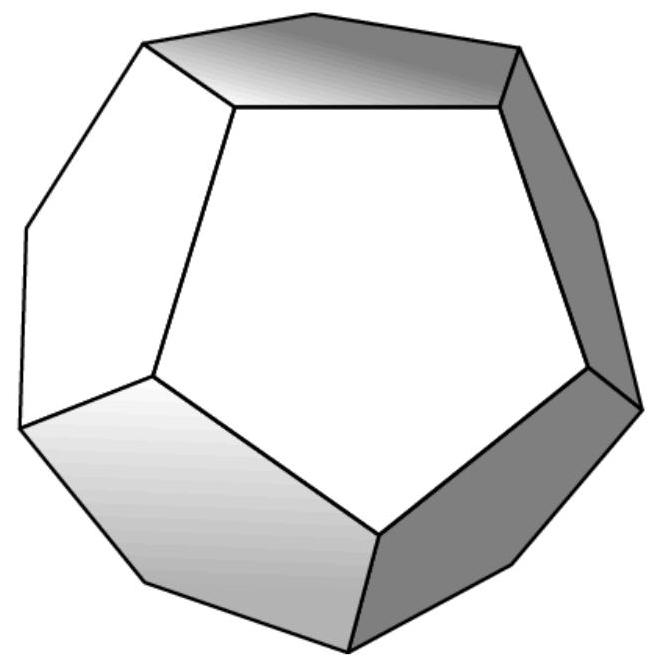
解法

由于我们从顶面出发，最终到达底面，且不能从下环回到上环，也不能重复访问任何面，因此整个路径必须依次经过:顶面、上环的一系列面、下环的一系列面，最后到底面。

在上环，我们首先要选择第一个访问的面，有5种选择。接着，我们决定在上环绕行多远再向下:顺时针绕行1、2、3或4个面，逆时针绕行1、2、3或4个面，或者立即下到下环而不在上环继续访问其他面，共9种选择。

然后，我们需选择下环的第一个面，有2种选择(因为每个上环面恰好与2个下环面相邻)；之后在下环的绕行方式同样有9种选择。最后一步即进入底面，完成整个行程。

把所有可选数目相乘，得到 $ 5 \cdot 9 \cdot 2 \cdot 9 = 1 $ (E)810

解法2

将面与顶点互换，即把面当作顶点、顶点当作面。于是，此题便与2016 AIME I第3题(https://artofproblemsolving.com/wiki/index.php/2016_AIME_I_Problems/Problem_3)相同，其答案为 $ \left( \mathbf{E}\right) {810} $ 。——Emathmaster

2020 AMC 10A 试题/第20题

以下题目同时出现在2020年AMC 12A第18题和2020年AMC 10A第20题，因此两道题均重定向至此页面。

问题

四边形 $ {ABCD} $ 满足 $ \angle {ABC} = \angle {ACD} = {90}^{ \circ },{AC} = {20}, $ 和 $ {CD} = {30} $ 。对角线 $ \overline{AC} $ 与 $ \overline{BD} $ 交于点 $ E, $ 且 $ {AE} = 5. $ 。求四边形 $ {ABCD} $ 的面积。

(A) 330 (B) 340 (C) 350 (D) 360 (E) 370

解法1(只需作一条高线)

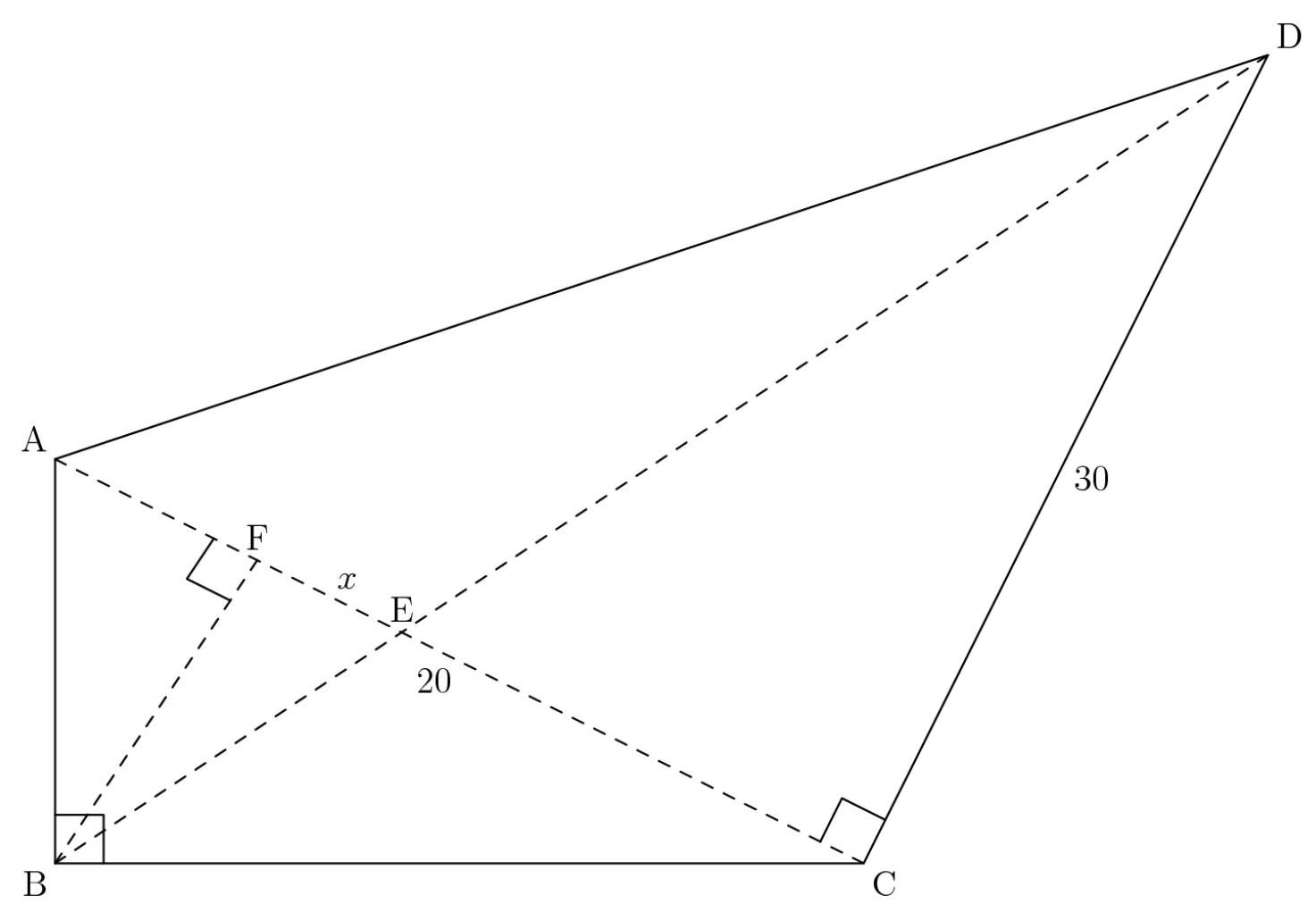
这一步画好示意图至关重要。由于 $ {AC} = {20} $ 且 $ {CD} = {30} $ ，我们得到 $ \left\lbrack {ACD}\right\rbrack = {300} $ 。现在需要求出 $ \left\lbrack {ABC}\right\rbrack $ ，才能算出整个四边形的面积。从 $ B $ 向 $ {AC} $ 作垂线，垂足记为 $ F $ 。设 $ {FE} = x $ 。因为 $ {AE} = 5 $ ，所以 $ {AF} = 5 - x $ 。通过作这条垂线，我们还能发现两个相似三角形: $ {BFE} $ 和 $ {DCE} $ 。由于 $ {EC} $ 是

$ {20} - 5 = {15} $ ，且 $ {DC} = {30} $ ，我们得到 $ {BF} = {2x} $ 。现在，如果我们重新绘制仅包含 $ {ABC} $ 的图，我们得到 $ {\left( 2x\right) }^{2} = \left( {5 - x}\right) \left( {{15} + x}\right) $ 。接下来，展开、化简并除以最大公因数(GCF)，我们得到 $ {x}^{2} + {2x} - {15} = 0 $ 。这可以因式分解为 $ \left( {x + 5}\right) \left( {x - 3}\right) $ 。由于长度不能为负， $ x = 3 $ 。由于 $ x = 3 $ ， $ \left\lbrack {ABC}\right\rbrack = {60} $ 。所以

\[ \left\lbrack {ABCD}\right\rbrack = \left\lbrack {ACD}\right\rbrack + \left\lbrack {ABC}\right\rbrack = {300} + {60} = {600} \]

(如果你是视觉学习者，我很抱歉，但现在你有了ciceronii提供的示意图)

~ 奥特曼的解法

$ \sim $ 图表由ciceronii绘制

解法2(专业猜题策略)

我们知道大三角形的面积为300。利用选项可知小三角形的面积是10的倍数，因此两直角边的乘积为

20的倍数。假设两条直角边分别为 $ \sqrt{20a} $ 和 $ \sqrt{20b} $ ，由于斜边为20，我们得到 $ a + b = {20} $ 。尝试较小的整数，当 $ a = 2 $ 和 $ b = {18} $ 时， $ {ab} $ 确实是一个完全平方数。因此三角形的面积为60，所以答案是(D) 360

~tigershark22~(由HappyHuman编辑)

解法3(坐标法)

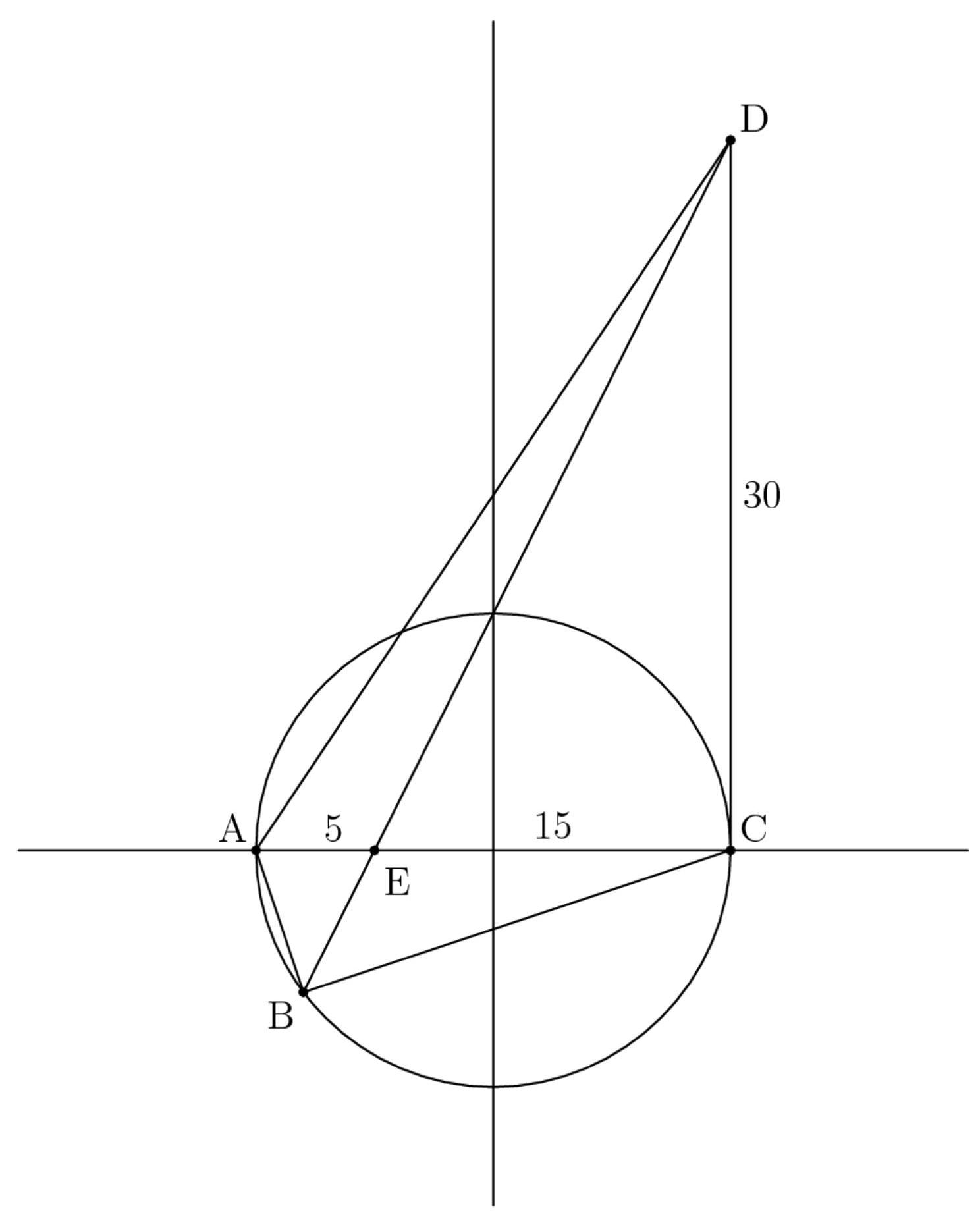
设这些点依次为 $ A\left( {-{10},0}\right) $ 、 $ B\left( {x, y}\right) $ 、 $ C\left( {{10},0}\right) $ 、 $ D\left( {{10},{30}}\right) $ 和 $ E\left( {-5,0}\right) $ 。由于 $ B $ 位于直线 $ {DE} $ 上，可知 $ y = {2x} + {10} $ 。此外，由于 $ \angle {ABC} = {90}^{ \circ } $ ， $ B $ 位于以 $ {AC} $ 为直径的圆上，因此 $ {x}^{2} + {y}^{2} = {100} $ 。联立这些方程解 $ x $ 和 $ y $ ，得到两组解(0,10)和(-8,-6)。我们立即舍去(0,10)这一组，因为 $ y $ 应为

负数。于是，我们得出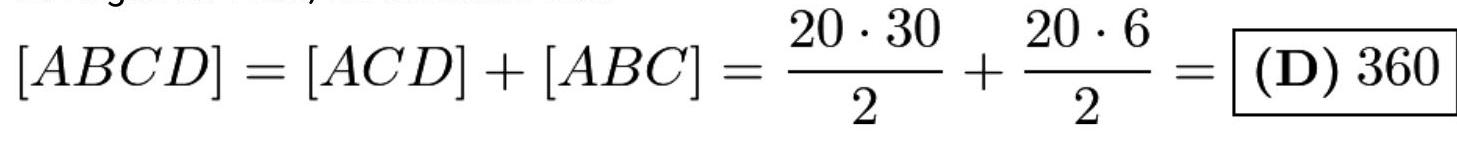

解法4(三角法)

设 $ \angle C = \angle {ACB} $ 和 $ \angle B = \angle {CBE}. $ ，在 $ \bigtriangleup {BCE} $ 上应用正弦定理，得到

\[ \frac{BE}{\sin C} = \frac{CE}{\sin B} = \frac{15}{\sin B} \]

再在 $ \bigtriangleup {ABE} $ 上应用正弦定理，得到

\[ \frac{BE}{\sin \left( {{90} - C}\right) } = \frac{5}{\sin \left( {{90} - B}\right) } = \frac{BE}{\cos C} = \frac{5}{\cos B}. \]

两式相除得 $ \tan B = 3\tan C. $ 。现在，

\[ \tan \angle {CED} = 2 = \tan \angle B + \angle C = \frac{4\tan C}{1 - 3{\tan }^{2}C} \]

解该二次方程，取正根(C为锐角)，得 $ \tan C = \frac{1}{3} $ 。因此，若 $ {AB} = a, $ ，则 $ {BC} = {3a} $ 且 $ \left\lbrack {ABC}\right\rbrack = \frac{3{a}^{2}}{2}. $ 。由勾股定理， $ {10}{a}^{2} = {400} \Leftrightarrow \frac{3{a}^{2}}{2} = {60} $ ，答案为 $ {300} + {60} \Leftrightarrow $ (D)

(此解法不完整，请哪位补充——Lingjun)已由kc5170完成LaTeX编辑

2020 AMC 10A 试题/第21题

题目

存在唯一一个严格递增的非负整数序列 $ {a}_{1} < {a}_{2} < \ldots < {a}_{k} $ ，使得

\[ \frac{{2}^{289} + 1}{{2}^{17} + 1} = {2}^{{a}_{1}} + {2}^{{a}_{2}} + \ldots + {2}^{{a}_{k}}. \]

求 $ k $ 的值？

(A) 117 (B) 136 (C) 137 (D) 273 (E) 306

解法1

首先，将 $ {2}^{17} $ 替换为 $ a $ 。于是原方程变为 $ \frac{{a}^{17} + 1}{a + 1} = {a}^{16} - {a}^{15} + {a}^{14}\ldots - {a}^{1} + {a}^{0} $ 。现在仅考虑 $ {a}^{16} - {a}^{15} $ ，它等于 $ {a}^{15}\left( {a - 1}\right) = {a}^{15} * \left( {{2}^{17} - 1}\right) $ 。注意到 $ {2}^{17} - 1 $ 等于 $ {2}^{16} + {2}^{15} + \ldots + 1 $ ，因为几何级数求和公式为 $ \frac{{a}^{n} - 1}{a - 1} $ 。因此，可以看出 $ {a}^{16} - {a}^{15} $ 是17个不同2的幂次之和。对 $ {a}^{14} - {a}^{13},{a}^{12} - {a}^{11},\ldots ,{a}^{2} - {a}^{1} $ 的每一对应用同样的方法，可知每一对都是17个不同2的幂次之和。于是得到 $ {17} * 8 = {136} $ 。但还需计入 $ {a}^{0} $ 这一项。因此，答案为 $ {136} + 1 = (\mathbf{C}\mathbf{)}{137} $ 。

~seanyoon777

解法2

(与解法1类似)设 $ x = {2}^{17} $ 。则 $ {2}^{289} = {x}^{17} $ 。左侧可改写为 $ \frac{{x}^{17} + 1}{x + 1} = {x}^{16} - {x}^{15} + \cdots + {x}^{2} - x + 1 = \left( {x - 1}\right) \left( {{x}^{15} + {x}^{13} + \cdots + {x}^{1}}\right) + 1 $ 。将 $ {2}^{17} $ 代回

替换 $ x $ ，我们得到 $ \left( {{2}^{17} - 1}\right) \left( {{2}^{15.17} + {2}^{13.17} + \cdots + {2}^{1 \cdot {17}}}\right) + 1 = \left( {{2}^{16} + {2}^{15} + \cdots + {2}^{0}}\right) ({2}^{{15} \cdot {17}} + {2}^{{13} \cdot {17}} + \cdots + {2}^{1.1} $ 。展开后，将出现 $ {17} \cdot 8 + 1 = {137} $ 项。因此，答案为 $ \left( {\mathbf{C}}\right) {137} $

解法3(直观)

两边同乘 $ {2}^{17} + 1 $ ，得到

\[ {2}^{289} + 1 = {2}^{{a}_{1}} + {2}^{{a}_{2}} + \ldots + {2}^{{a}_{k}} + {2}^{{a}_{1} + {17}} + {2}^{{a}_{2} + {17}} + \ldots + {2}^{{a}_{k} + {17}}. \]

注意到 $ {a}_{1} = 0 $ ，因为左侧有1。然而，右侧因 $ {2}^{{a}_{1} + {17}} $ 而多出一项 $ {2}^{18} $ 。为消去它，令 $ {a}_{2} = {18} $ 。两个 $ {2}^{18} $ 合并为 $ {2}^{19} $ ，于是令 $ {a}_{3} = {19} $ 。依此类推，直至 $ {a}_{18} = {34} $ 。此时，所有不需要的部分缩并为 $ {2}^{35} $ 。我们已拥有该项，因为我们设

$ {a}_{2} = {18} \Longrightarrow {a}_{2} + {17} = {35} $ 。此后所有项将自动缩并为 $ {2}^{52} $ 。因此令 $ {a}_{19} $ 为52。

可见，我们需一次添加 $ {17}{a}_{n} $ ，然后“等待”其自动缩并接下来的17个数，依此类推，直至 $ {2}^{289} $ 。只需在17的奇数倍与偶数倍之间添加 $ {a}_{n} $ 。289以下最大的17的偶数倍是 $ {17} \cdot {16} $ ，故总共需添加 $ {17} \cdot 8{a}_{n} $ 。然而别忘了最初设 $ {a}_{1} = 0 $ ，因此答案为 $ {17} \cdot 8 + 1 = $ (C)137

解法4

注意该表达式略小于 $ {2}^{272} $ 。显然，选项(D)与(E)无意义，因为273项的最小和为 $ {2}^{273} - 1 $ 。(A)也毫无道理。(B)与(C)仅差1，但表达式为奇数，必含 $ {2}^{0} = 1 $ ，而(C)大1，故答案为 $ \left( \mathbf{C}\right) {137} $ 。~LCZ

解法5

为简化表达式，#表示16个连续的0。

用二进制思考此题。我们有

$ {1\# 0\# 0\# 0\# 0\# 0\# 0\# 0\# 0\# 0\# 0\# 0\# 0\# 0\# 0\# 0\# 0\# 0\# 1}{1}_{2} $

$ 1\# {1}_{2} $

注意 $ \left( {{2}^{17} + 1}\right) \left( {{2}^{0} + {2}^{34} + {2}^{68} + \cdots + {2}^{272}}\right) = {2}^{0}\left( {{2}^{17} + 1}\right) + {2}^{34}\left( {{2}^{17} + 1}\right) + {2}^{68}\left( {{2}^{17} + 1}\right) + \cdots {2}^{272}\left( \right. $

$ = {1\# 1\# 1\# 1\# 1\# 1\# 1\# 1\# 1\# 1\# 1\# 1\# 1\# 1\# 1\# 1\# 1\# 1\# 1\# 1\# 1} $

$ ({2}^{17} + 1)({2}^{17} + {2}^{51} + {2}^{85} + \cdots + {2}^{255}) = {2}^{17}({2}^{17} + 1) + {2}^{51}({2}^{17} + 1) + {2}^{85}({2}^{17} + 1) + \cdots {2}^{25} $

= 1#1#1#1#1#1#1#1#1#1#1#1#1#1#1#1#1#1#0

由于

]#1#1#1#1#1#1#1#1#1#1#1#1#1#1#1#1#1#1#1

$ - \;\begin{matrix} 1 & \# & 1 & \# & 1 & \# & 1 & \# & 1 & \# & 1 & \# & 1 & \# & 1 & \# & 1 & \# & 1 & \# & 1 & \# & 1 & \# & 1 & \# & 1 & \# & 1 & \# & 1 & \# & 1 & \# & 0 \end{matrix} $

$ = 1\# 0\# 0\# 0\# 0\# 0\# 0\# 0\# 0\# 0\# 0\# 0\# 0\# 0\# 0\# 0\# 1\# 1 $

这意味着

$ \left( {{2}^{17} + 1}\right) \left( {{2}^{0} + {2}^{34} + {2}^{68} + \cdots + {2}^{272}}\right) - \left( {{2}^{17} + 1}\right) \left( {{2}^{17} + {2}^{51} + {2}^{85} + \cdots + {2}^{255}}\right) = {2}^{289} $

所以 $ \frac{{2}^{289} + 1}{{2}^{17} + 1} = ({2}^{0} + {2}^{34} + {2}^{68} + \cdots + {2}^{272}) - ({2}^{17} + {2}^{51} + {2}^{85} + \cdots + {2}^{255}) $

$ = {2}^{0} + \left( {{2}^{34} - {2}^{17}}\right) + \left( {{2}^{68} - {2}^{51}}\right) + \cdots + \left( {{2}^{272} - {2}^{255}}\right) $

将每对形如 $ {2}^{n + {17}} - {2}^{n} $ 的数用二进制表示，我们得到

$ {10000000000000000000}\cdots {0}_{2} $

$ {10}\cdots {0}_{2} $

$ = \left\lbrack \begin{matrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 0 \\ \cdots \\ \end{matrix}\right\rbrack \cdot {0}_{2}^{ - } $

或

$ {2}^{n + {17}} - {2}^{n} = {2}^{n + {16}} + {2}^{n + {15}} + {2}^{n + {14}} + \cdots + {2}^{n} $

这意味着每一对包含17个形如 $ {2}^{n} $ 的项。

由于共有8对，因此总共有 $ 8 \cdot {17} = {136} $ 项。再计入未配对的 $ {2}^{0} $ 项，

我们共有 $ {136} + 1 = \left( {\mathbf{C}\mathbf{\sum }}\right) {137} $ 项。-emerald_block

视频解析

https://youtu.be/Ozp3k2464u4

~IceMatrix

另见

2020 AMC 10A 第22题

题目

有多少个正整数 $ n \leq {1000} $ 满足

\[ \left\lfloor \frac{998}{n}\right\rfloor + \left\lfloor \frac{999}{n}\right\rfloor + \left\lfloor \frac{1000}{n}\right\rfloor \]

不能被3整除？(回忆: $ \lfloor x\rfloor $ 表示不大于 $ x $ 的最大整数。)

(A) 22 (B) 23 (C) 24 (D) 25 (E) 26

解法1(分类讨论)

表达式:

\[ \left\lfloor \frac{998}{n}\right\rfloor + \left\lfloor \frac{999}{n}\right\rfloor + \left\lfloor \frac{1000}{n}\right\rfloor \]

解答:

令 $ a = \left\lfloor \frac{998}{n}\right\rfloor $

由于 $ \frac{1000}{n} - \frac{998}{n} = \frac{2}{n} $ ，对于任意整数 $ n \geq 2 $ ，最大差值

在应用 $ \lfloor x\rfloor $ 函数之前，最大项与最小项之差小于或等于1，因此应用该函数后，各项的取值范围必须为1或更小。

这意味着对于每一个整数 $ n \geq 2 $ ， $ \bullet $ 如果 $ \frac{998}{ - } $ 是整数且 $ n \neq 2 $ ，则上述表达式中的三项必须为 $ \left( {a, a, a}\right) , $ $ \bullet $ ；如果 $ \frac{998}{n} $ 是整数，因为 $ n = 2 $ ，则 $ \frac{1000}{n} $ 将是整数且比 $ \frac{998}{n} $ 大1；因此表达式中的三项必须为 $ \left( {a, a, a + 1}\right) $ ， $ \bullet $ ；如果 $ \frac{999}{\infty } $ 是整数，则上述表达式中的三项必须为 $ \left( {a, a + 1, a + 1}\right) $ ，

如果 $ \frac{1000}{n} $ 是整数，则上述表达式中的三项必须为 $ \left( {a, a, a + 1}\right) $ 和 $ \bullet $ ；如果 $ \left\{ {\frac{998}{n},\frac{999}{n},\frac{1000}{n}}\right\} $ 中没有一个是整数，则上述表达式中的三项必须为(a, a, a)。

最后一条陈述成立，因为要使各项不同，区间 $ \left( {\frac{998}{n},\frac{999}{n}}\right) $ 或区间 $ \left( {\frac{999}{n},\frac{1000}{n}}\right) $ 中必须存在某个整数。然而，这意味着将该整数乘以 $ n $ 后应得到一个新的整数，且该整数严格介于998与999之间或999与1000之间，但由于不存在这样的整数，各项不可能不同，因此必须相等。

$ \bullet $ 请注意， $ n = 1 $ 不成立；要证明这一点，只需在表达式中将 $ n $ 替换为 1。这样我们得到

\[ \left\lfloor \frac{998}{1}\right\rfloor + \left\lfloor \frac{999}{1}\right\rfloor + \left\lfloor \frac{1000}{1}\right\rfloor = {998} + {999} + {1000} = {2997} = {999} \cdot 3 \]

能被3整除。

现在，我们测试上述列出的五种情况(其中 $ n \geq 2 $ )

案例1: $ n $ 整除998且 $ n \neq 2 $

如上所述，表达式中的三项为(a, a, a)，因此它们的和为 $ {3a} $ ，可被3整除。因此，第一种情况不成立。

情况2: $ n $ 整除998且 $ n = 2 $

如上所述，在此情况下各项必须 $ \left( {a, a, a + 1}\right) $ ，这意味着总和为 $ {3a} + 1 $ ，因此该表达式不能被3整除。因此，这是1个有效的情况。

情况3: $ n $ 整除999

因为 $ n $ 整除999，所以 $ n $ 的可能取值个数与999的因数个数相同。

999= $ {3}^{3} \cdot {37}^{1} $ 。因此，999的总因数个数为 $ 4 \cdot 2 = 8 $ 。

然而，我们必须减去1，因为 $ n = 1 $ 的情况无效，如前所述。这样就剩下 $ 8 - 1 = 7 $ 种情况。情况4: $ n $ 整除1000

因为 $ n $ 整除1000，所以 $ n $ 的可能取值个数与1000的因数个数相同。

1000= $ {5}^{3} \cdot {2}^{3} $ 。因此，1000的总因数个数为 $ 4 \cdot 4 = {16} $ 。

同样，我们必须减去1，因此剩下 $ {16} - 1 = {15} $ 种情况。我们还重复计算了因数2，因为它既被算作1000的因数，又被单独列为情况2。 $ {15} - 1 = {14} $ ，所以实际上共有14种有效情况。

情况5: $ n $ 不整除 $ \{ {998},{999},{1000}\} $ 中的任何一个

与情况1类似，表达式各项的值为(a, a, a)。总和为 $ {3a} $ ，可被3整除，因此该情况无效。

现在我们已经统计了所有情况，将它们相加。

\[ 0 + 1 + 7 + {14} + 0 = {22}\text{, so the answer is}\sigma \text{.}\sigma \text{.} \]

~dragonchomper，由emerald_block补充编辑

解法2(基本上是解法1的简化版)

注意此解法未统计大多数情况，因此可能不适用于其他问题

注意到只需统计1000和999的因数个数，并排除1。1000有16个因数，999有8个。相加得24，但需减去2，因为1

无效。

因此，答案是 $ {24} - 2 = \left( {\text{A},{22}}\right) $

-happykeeper，由dragonchomper补充编辑

2020 AMC 10A 第23题

以下题目同时出现在2020 AMC 12A 第20题和2020 AMC 10A

第23题，因此两道题目均重定向至此页面。

题目

设 $ T $ 为坐标平面上以 $ \left( {0,0}\right) ,\left( {4,0}\right) , $ 和 $ \left( {0,3}\right) . $ 为顶点的三角形。考虑平面的以下五种等距变换(刚性变换):绕原点逆时针旋转 $ {90}^{ \circ },{180}^{ \circ }, $ 和 $ {270}^{ \circ } $ ，关于 $ x $ 轴的反射，以及关于 $ y $ 轴的反射。在这125种由三个变换组成的序列(允许重复)中，有多少种序列能将 $ T $ 恢复到原始位置？(例如，先进行 $ {180}^{ \circ } $ 旋转，再关于 $ x $ 轴反射，再关于 $ y $ 轴反射，可将 $ T $ 恢复到原始位置；但先进行 $ {90}^{ \circ } $ 旋转，再关于 $ x $ 轴反射，再关于 $ x $ 轴反射，则不能将 $ T $ 恢复到原始位置。)

(A) 12 (B) 15 (C) 17 (D) 20 (E) 25

解答

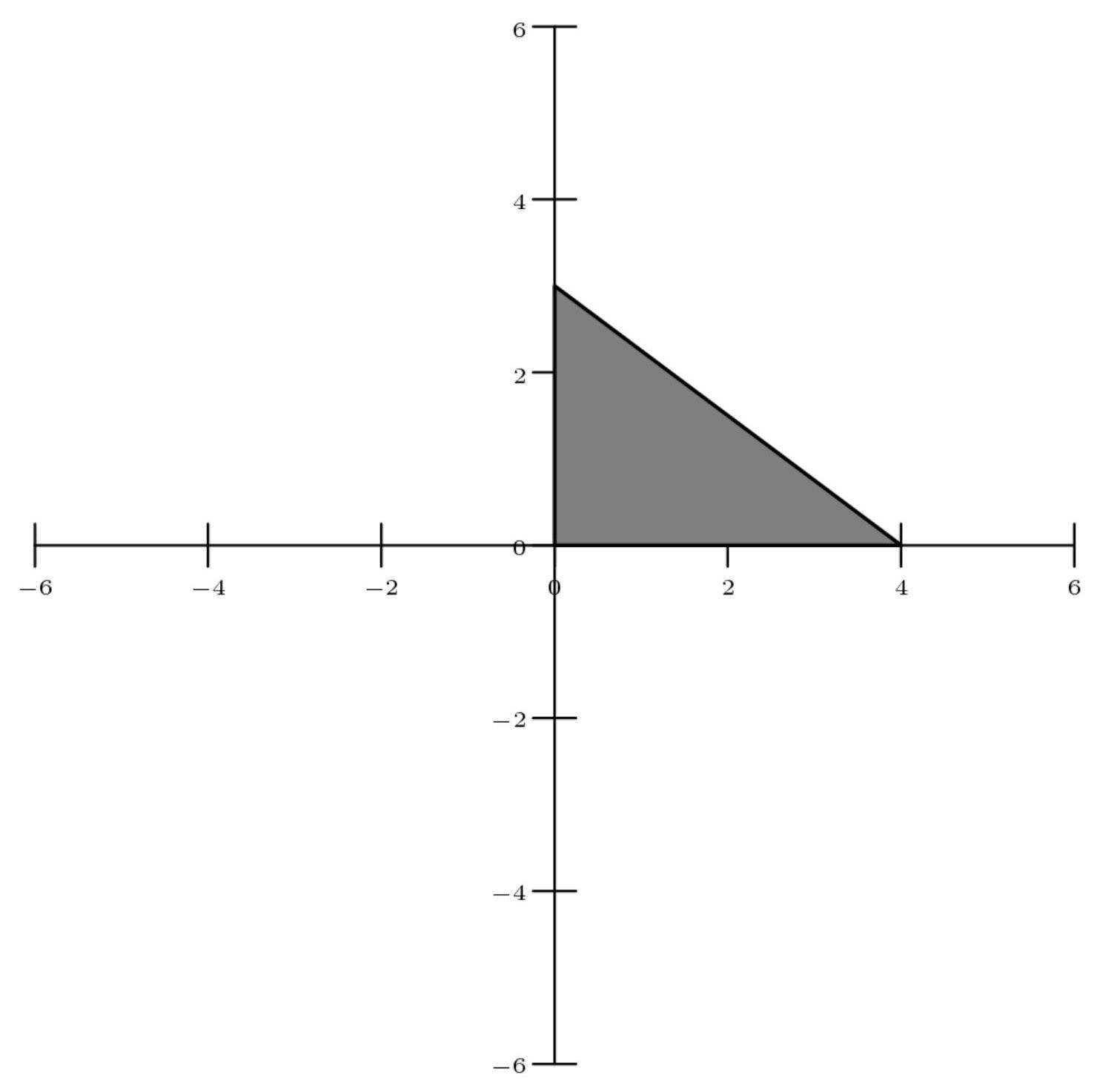
首先，我们所能做的任何运动组合都必须对 $ T $ 进行偶数次反射。这是因为每次反射 $ T $ 都会改变其方向。一旦 $ T $ 被翻转一次，任何旋转组合都无法将其恢复原位，因为它已成为镜像；然而，再次翻转会将其恢复到原始方向。由于我们仅允许3次变换，且其中反射次数必须为偶数，因此我们要么反射 $ T0 $ 次，要么反射2次。在此情况下，我们必须使用3次旋转才能将 $ T $ 恢复到原始位置。注意，我们的旋转集合 $ \{ {90}^{ \circ },{180}^{ \circ },{270}^{ \circ }\} $ 包含除 $ {0}^{ \circ } $ 外所有 $ {90}^{ \circ } $ 的倍数。我们可以从 $ \{ {90}^{ \circ },{180}^{ \circ },{270}^{ \circ }\} $ 中任选两个旋转 $ a, b $ ，且必存在唯一一个 $ c \equiv - a - b{\;(\operatorname{mod}\;{360}^{ \circ })} $ ，使得我们可以使用这三个旋转(a, b, c)，确保 $ a + b + c \equiv {0}^{ \circ }\;\left( {\operatorname{mod}\;{360}^{ \circ }}\right) $ 。这样，旋转组合 $ a, b, c $ 将产生一个完整的旋转。例如，若 $ a = b = {90}^{ \circ } $ ，则 $ c \equiv - {90}^{ \circ } - {90}^{ \circ } = - {180}^{ \circ }{\;(\operatorname{mod}\;{360}^{ \circ })} $ ，因此 $ c = {180}^{ \circ } $ ，且旋转组合 $ \left( {{90}^{ \circ },{90}^{ \circ },{180}^{ \circ }}\right) $ 产生一个完整的旋转。

唯一失败的情况是当 $ c $ 必须等于 $ {0}^{ \circ } $ 时。这种情况发生在(a, b)本身已构成一个完整旋转时，即

$ \left( {a, b}\right) = \left( {{90}^{ \circ },{270}^{ \circ }}\right) ,\left( {{180}^{ \circ },{180}^{ \circ }}\right) , $ 或 $ \left( {{270}^{ \circ },{90}^{ \circ }}\right) $ 。然而，我们只需从总数中减去这三种情况即可。从 $ \{ {90}^{ \circ },{180}^{ \circ },{270}^{ \circ }\} $ 中选择(a, b)有 $ 3 \cdot 3 = 9 $ 种可能，减去3种失败情况后，情况1剩下6种组合。

案例2:在T上的2次反射

在此情况下，我们首先排除出现两次相同反射的可能性。由于两次关于x轴的反射会将 $ T $ 映射回自身，若在这两次反射之前、之间或之后插入一次旋转，都会改变 $ T $ 的最终位置，这意味着任何包含两次关于x轴反射的组合都无法将 $ T $ 映射回自身。两次关于y轴的反射同理。

因此，我们必须进行一次关于x轴的反射、一次关于y轴的反射以及一次旋转。由于关于x轴的反射会改变y分量的符号，关于y轴的反射会改变 $ x $ 分量的符号，而 $ {180}^{ \circ } $ 旋转会同时改变两个分量的符号，这三个变换(按任意顺序)组合起来即可满足要求。因此，问题仅在于如何排列这三者，从而在情况2中给出 $ 3! = 6 $ 种组合。

综合两种情况，我们得到 $ 6 + 6 = $ (A) 12

解决方案2(改写方案1)

与之前的解法一样，请注意，由于方向性，我们必须有0次或2次反射(reflection)，因为反射会改变方向，而旋转无法修正这一点。我们还知道，不能出现两次相同的反射，否则将产生净无变化，从而需要恒等旋转(identity rotation)。

假设没有反射。为简化起见，将 $ {90}^{ \circ } $ 记为1， $ {180}^{ \circ } $ 记为2， $ {270}^{ \circ } $ 记为3。我们需要从中选取3个数的组合，使其和为4或8(0和12不可能，因为最小和为3，最大和为9)。4可通过任意排列得到，8也可通过任意排列得到。此情形共有种方式。

假设存在两个反射。如前所述，它们必须不同，因此若不进行任何旋转，三角形将被映射到原点的另一侧。然而我们还剩一次旋转可用，唯一能使其回到初始位置的旋转是2，即 $ {180}^{ \circ } $ ，亦即关于原点的反射。因此，由于所有3种变换互不相同，且这些变换可任意顺序应用(因为它们可交换，可想象为象限操作)，总共有6种方式。

2020 AMC 10A 试题/第24题

问题

令 $ n $ 为大于1000的最小正整数，使得

$ \gcd \left( {{63}, n + {120}}\right) = {21} $ 和 $ \gcd \left( {n + {63},{120}}\right) = {60} $ 。

$ n $ 的各位数字之和是多少？

(A) 12 (B) 15 (C) 18 (D) 21 (E) 24

解决方案 1

我们知道 $ {gcd}\left( {{63}, n + {120}}\right) = {21} $ ，因此可以写成 $ n + {120} \equiv 0{\;(\operatorname{mod}\;{21})} $ 。化简后得到 $ n \equiv 6{\;(\operatorname{mod}\;{21})} $ 。同理，可写成 $ n + {63} \equiv 0{\;(\operatorname{mod}\;{60})} $ ，或 $ n \equiv - 3{\;(\operatorname{mod}\;{60})} $ 。解这两个同余式， $ n \equiv {237}{\;(\operatorname{mod}\;{420})} $ ，根据中国剩余定理(Chinese Remainder Theorem)，这是唯一解。现在，题目要求大于1000的最小正整数，我们求得最小解为 $ n = {1077} $ 。然而，我们尚未考虑 $ {gcd}\left( {{63}, n + {120}}\right) = {63} $ 或 $ {gcd}\left( {n + {63},{120}}\right) = {120} $ 的情况。 $ {1077} + {120} \equiv 0 $ ’(mod63)，因此我们尝试 $ n = {1077} + {420} = {1497} $ 。 $ {1497} + {63} \equiv 0{\;(\operatorname{mod}\;{120})} $ ，于是再次给 $ n $ 加上420。结果 $ n = {1497} + {420} = {1917} $ 确实满足原条件，故答案为 $ 1 + 9 + 1 + 7 = $ (C)18 解法2(暴力枚举)

已知 $ \gcd \left( {{63}, n + {120}}\right) = {21} $ 和 $ \gcd \left( {n + {63},{120}}\right) = {60} $ 。由此可知 $ n + {120} $ 能被21整除但不能被63整除，且 $ n + {63} $ 能被60整除但不能被120整除。首先，我们找出满足 $ n $ 条件且能被21整除的最小 $ n + {120} $ ，即1134，于是 $ n = {1014} $ 。接着，我们不断加21，直到得到一个满足第二个方程的数。这个数是1917，其各位数字之和为(C) 18

-午夜

解法3(暴力但更糟糕)

假设 $ n $ 是一个四位数。那么 $ n = {abcd} $ ，其中 $ a $ 、 $ b $ 、 $ c $ 、 $ d $ 分别表示该数的各位数字(不要与 $ a * b * c * d $ 混淆)。根据题意， $ {gcd}\left( {{63}, n + {120}}\right) = {21} $ 且 $ {gcd}\left( {n + {63},{120}}\right) = {60} $ 。因此我们知道 $ d = 7 $ ( $ n $ 的个位数字)。这意味着 $ {12} + {abc} \equiv 0{\;(\operatorname{mod}\;7)} $ 且 $ 7 + {abc} \equiv 0{\;(\operatorname{mod}\;6)} $ 。接下来我们可以暴力枚举。我们只需找出所有数对(x, y)，使得 $ x $ 是7的倍数且比某个6的倍数大5。关于 $ {12} + {abc} $ 的方程为 $ {42} * j + {35} = x $ ，而关于 $ 7 + {abc} $ 的方程为 $ {42} * j + {30} = y $ ，其中 $ j $ 为任意整数。我们将该值代入，直到得到使 $ n = {abc7} $ 满足原题条件的 $ {abc} $ (记住 $ {abc} > {100} $ )。经过几分钟的暴力计算，我们发现 $ {abc} = {191} $ 成立。因此 $ n = {1917} $ ，这意味着其各位数字之和为 $ \mid \left( \mathrm{C}\right) {18} $ 。

~宝蓝

2020 AMC 10A 第25题

以下题目同时出现在2020 AMC 12A第23题和2020 AMC 10A第25题，因此两题均重定向至此页面。

题目

Jason掷三颗公平的六面骰子。然后他观察点数，并选择其中任意子集(可为空集，也可为全部三颗骰子)进行重掷。重掷后，若三颗骰子朝上面点数之和恰好为7，则获胜。Jason总是采取最优策略以最大化获胜概率。求他选择恰好重掷两颗骰子的概率。

(A) $ \frac{7}{36} $ (B) $ \frac{5}{24} $ (C) $ \frac{2}{9} $ (D) $ \frac{17}{72} $ (E) $ \frac{1}{4} $

解法1

考虑掷两颗骰子得到和为 $ s $ 的概率，其中 $ s \leq 7 $ 。满足条件的组合有 $ s - 1 $ 种，即 $ \left( {1, s - 1}\right) ,\left( {2, s - 2}\right) ,...,\left( {s - 1,1}\right) $ ，而所有可能组合共 $ {6}^{2} = {36} $ 种。因此概率为 $ \frac{s - 1}{36} $ 。

因此，若一颗骰子点数为 $ a $ 且Jason重掷另外两颗骰子，则获胜概率为 $ \frac{7 - a - 1}{36} = \frac{6 - a}{36} $ 。

为了最大化获胜概率， $ a $ 必须最小化。这意味着若Jason重掷两颗骰子，他必须选择点数最大的两颗骰子进行重掷。

因此，我们可以令 $ a \leq b \leq c $ 为三颗骰子的点数，分别记为 $ A $ 、 $ B $ 和 $ C $ 。考虑 $ a + b < 7 $ 的情况。若 $ a + b + c = 7 $ ，则无需重掷任何骰子。否则，若只重掷一颗骰子，我们可以重掷 $ C $ ，期望掷出能使三颗骰子总和为7的点数，这种情况发生的概率为 $ \frac{1}{6} $ 。若重掷两颗骰子，我们将重掷 $ B $ 和 $ C $ ，获胜概率为 $ \frac{6 - a}{36} $ ，如前所述。然而， $ \frac{1}{6} > \frac{6 - a}{36} $ ，因此当 $ a + b < 7 $ 时，重掷一颗骰子总是比重掷两颗骰子更优。现在考虑 $ a + b \geq 7 $ 的情况。此时重掷一颗骰子无法帮助我们获胜，因为三颗骰子的总和将始终大于7。若重掷两颗骰子，获胜概率仍为 $ \frac{6 - a}{36} $ 。若要计算重掷全部三颗骰子时的获胜概率，我们可以假设每颗骰子初始为1点，然后计算将剩余4点分配到三颗骰子上的方式数。根据星与棒(Stars and Bars)方法，共有 $ \left( \begin{array}{l} 6 \\ 2 \end{array}\right) = {15} $ 种分配方式。

这使得获胜的概率为 $ \frac{15}{{6}^{3}} = \frac{5}{72} $ 。

为了让掷两个骰子比掷三个骰子更有利，

\[ \frac{6 - a}{36} > \frac{5}{72} \rightarrow a \leq 3 \]

因此，当且仅当 $ a \leq 3 $ 且 $ a + b \geq 7 $ 时，重掷两颗骰子是最优策略。满足这些条件的三元组(a, b, c)及其可排列方式共有 $ \left( {3,4,4}\right) \rightarrow 3 $ 种， $ \left( {3,4,5}\right) \rightarrow 6 $ 种。

$ \left( {3,4,6}\right) \rightarrow 6 $ 种方式。 $ \left( {3,5,5}\right) \rightarrow 3 $ 种方式。 $ \left( {3,5,6}\right) \rightarrow 6 $ 种方式。

$ \left( {3,6,6}\right) \rightarrow 3 $ 种方式。 $ \left( {2,5,5}\right) \rightarrow 3 $ 种方式。 $ \left( {2,5,6}\right) \rightarrow 6 $ 种方式。

$ \left( {2,6,6}\right) \rightarrow 3 $ 种方式。 $ \left( {1,6,6}\right) \rightarrow 3 $ 种方式。

在 $ {6}^{3} = \underline{216} $ 种可能性中，有 $ 3 + 6 + 6 + 3 + 6 + 3 + 3 + 6 + 3 + 3 = {42} $ 种情况下重掷两颗骰子是最优策略，因此概率

Jason将重掷两个骰子的概率是 $ \frac{42}{216} = $ (A) $ \frac{7}{36} $

解决方案 2

我们计算分子。如果Jason已经掷出总和为7，他将不再捡起任何骰子。我们需要假设他一开始没有7。如果Jason决定捡起所有骰子重新掷，根据星条法(Stars and Bars，或随便什么方法……)，会有2条和4星(其中3星必须保证，因为每次掷骰至少为1)，概率为 $ \frac{15}{216} = \frac{2.5}{36} $ 。如果Jason捡起2颗骰子并留下一颗显示 $ k $ ，他需要另外两颗骰子之和为 $ 7 - k $ ，这种情况发生的概率为

\[ \frac{6 - k}{36} \]

对于整数 $ 1 \leq k \leq 6 $ 。如果掷出的点数不是7，Jason 会恰好重掷一颗骰子，只要剩下的两颗骰子之和小于7，因为这会给他带来 $ \frac{1}{6} $ 的概率，这个概率比所有其他情况都大，除非他一开始就掷出了7。我们有

\[ \frac{1}{6} > \underline{\frac{5,4,3}{36}} > \frac{2.5}{36} > \frac{2,1,0}{36}. \]

我们统计下划线部分出现的次数作为分子，同时不破坏比它更大的概率。设 $ a $ 为保留的点数。我们知道 $ a $ 最多为3，因为若为4，Jason 会重掷所有骰子。当 $ a = 1 $ 时，有3种选择决定它出现在 $ 1\mathrm{{st}},2\mathrm{{nd}} $ 还是 $ 3\mathrm{{rd}} $ ，此时另外两颗骰子必须至少为6(否则他只会重掷1颗)。这给出 $ 3 \cdot {1}^{2} = 3 $ 种方式。类似地， $ a = 2 $ 给出 $ 3 \cdot {2}^{2} = {12} $ ，因为2可以出现在3个位置，且另外两颗骰子至少为5。 $ a = 3 $ 给出 $ 3 \cdot {3}^{2} = {27} $ 。相加得到分子为42。分母为 $ {6}^{3} = {216} $ ，因此我们有 $ \frac{42}{216} = \left( A\right) \frac{7}{36} $

视频解析

https://youtu.be/3W4jOpCiBx8 - AwesomeMath_Life 另见